12-06 Uniqueness in L1 penalized problems

다음의 \(L1\) penalized linear regression 문제는 lasso problem이란 이름으로도 잘 알려져 있다.

\[\begin{align} &&&\hat{\beta} \in \text{argmin}_{\beta \in \mathbb{R}^p} \frac{1}{2} \| y - X\beta \|^2_2 + \lambda \|\beta\|_1, \qquad \\\\ && \text{ --- (1) } &\text{given } y \in \mathbb{R}^n, \\\\ &&& \text{ a matrix } X \in \mathbb{R}^{n \text{ x } p} \ \text{ of predictor variables,} \\\\ &&& \text{and a tuning parameter} \lambda \ge 0. \end{align}\]

위 Lasso problem은 \(rank(X) = p\)일 때 strictly convex가 되면서 유일한 solution을 갖는다. 반면, \(rank(X) < p\)일때(strictly convex가 아닐때)는 무수히 많은 solution을 갖을 수도 있게된다 (Reference: Underdetermined system). - 참고로 변수(p)의 갯수가 관측(n)의 갯수보다 크다면, \(rank(X)\)는 반드시 \(p\)보다 작아진다.
흥미롭게도 어떤 특수한 경우에 대해서는 \(X\)의 차원에 상관없이 Lasso problem이 유일한 해를 가짐이 보장된다 [13].

Theorem: 함수 \(f\)가 미분가능하며 strictly convex이고, \(\lambda > 0\)이며 \(X \in \mathbb{R}^{n \text{ x } p}\)가 \(\mathbb{R}^{np}\)에 대한 어떤 continuous probability distribution을 따를 때, 다음 최적화 문제는 항상 유일한(unique) solution을 갖는다. 또한 그 solution은 많아봐야 \(min\{n,p\}\)만큼의 nonzero components로 구성된다. 이때, \(X\)의 차원에 대한 제약은 없다. (즉, p » n일때도 유효)

Basic facts and the KKT conditions

Lemma 1. 임의의 \(y, X, \lambda \ge 0\)에 대해 lasso problem (1)은 다음과 같은 성질을 갖는다.

1. 유일한 solution을 갖거나 혹은 무한히 많은 수의 solution을 갖는다.
2. 모든 lasso solution \(\hat{\beta}\)는 같은 \(X\hat{\beta}\)값을 갖는다.
3. \(\lambda > 0\)일때, 모든 lasso solution \(\hat{\beta}\)는 같은 \(l_1\) norm을 갖는다 (\(\|\hat{\beta}\|_1\)).

\[\text{ }\]

Proof.

1. 만약 (1)이 두 개의 solution \(\hat{\beta}^{(1)}\), \(\hat{\beta}^{(2)}\)를 가질때, 임의의 \(0 < \alpha < 1\)에 대해 \(\alpha \hat{\beta}^{(1)} + (1 - \alpha) \hat{\beta}^{(2)}\) 또한 solution이 되므로 무수히 많은 solution이 존재하게 된다.
   
2. & 3. 두 개의 solution \(\hat{\beta}^{(1)}\), \(\hat{\beta}^{(2)}\)가 있다고 가정해보자. 이때 optimal value를 \(c^\star\)라고 하면, 어떤 임의의 solution인 \(\alpha \hat{\beta}^{(1)} + (1 - \alpha) \hat{\beta}^{(2)}\) (\(0 < \alpha < 1\))에 대해 아래의 등식을 항상 만족해야만 한다.

\[\begin{align} &\frac{1}{2} \| y - X(\alpha \hat{\beta}^{(1)} + (1 - \alpha) \hat{\beta}^{(2)}) \|_2^2 + \lambda \| \alpha \hat{\beta}^{(1)} + (1 - \alpha) \hat{\beta}^{(2)} \|_1 \\ & = \alpha c^\star + (1-\alpha) c^\star = c^\star \end{align}\]

위 등식을 만족하기 위해서는 임의의 solution \(\hat{\beta}\)에 대해 \(X\hat{\beta}\)은 항상 같은 값을 가져야 하고, \(\lambda > 0\)일때 \(\| \hat{\beta} \|_1\) 값 또한 항상 같아야 한다.

다시 처음으로 돌아가, lasso problem (1)에 대한 KKT conditions는 아래와 같다.

\[\begin{align} &&X^T (y - X\hat{\beta}) = \lambda \gamma, \qquad \text{ --- (2)} \\\\ &&\gamma_i \in \begin{cases} \{ sign(\hat{\beta_i}) \} & if \hat{\beta_i} \neq 0 \\\\ [-1, 1] & if \hat{\beta_i} = 0, \end{cases} \\\\ &&\text{for } i = 1, \dots, p. \text{ --- (3)} \\\\ &&\text{Here } \gamma \in \mathbb{R}^p \text{ is called a subgradient of the function } \\ &&f(x) = \| x \|_1 \text{ evaluated at } x = \hat{\beta}. \end{align}\]

즉, (1)의 solution인 \(\hat{\beta}\)는 어떤 \(\gamma\)에 대해 (2) 와 (3)을 만족한다.

위에서 얻은 KKT conditions를 이용하여 lasso solution에 대한 조건을 좀 더 명시적인 형태로 변환해보도록 하자. 이후의 진행에서는 유도의 간결함을 위해 \(\lambda > 0\)를 가정하도록 한다. 우선 equicorrelation set \(\mathcal{E}\)을 다음과 같이 정의한다. \(\mathcal{E}\)는 \(\hat{\beta}_i \neq 0\)인 모든 인덱스 \(i\)와 \(\hat{\beta}_j = 0\)이면서 \(\vert\gamma_j\vert = 1\)인 모든 인덱스 \(j\)를 원소로 가진 집합이다.

\[\mathcal{E} = \{ i \in \{1, \dots, p \} : \vert X_i^T (y - X\hat{\beta}) \vert = \lambda \}. \qquad \text{ --- (4)}\]

또한 equicorrelation sign \(s\)를 다음과 같이 정의한다. 여기서 \(X_\mathcal{E}\)는 행렬 X에서 \(i \in \mathcal{E}\)인 column \(i\) 외의 모든 column을 0 벡터로 교체한 행렬을 의미한다.

\[s = sign(X^T_\mathcal{E} (y -X\hat{\beta}). \qquad \text{ --- (5)}\]

여기서 \(\mathcal{E}, s\)는 \(\gamma\)에 대해 다음과 같이 표현할 수 있다: \(\mathcal{E} = \{i \in \{1, \dots, p \} : \vert \gamma_i \vert = 1 \}\) and \(s = \gamma_{\mathcal{E}}\). 또한 Lemma1-2에 의해 \(X\hat{\beta}\)는 유일한 값을 가지므로 이는 \(\mathcal{E}\), \(s\)이 유일함을 암시한다.

(3)의 subgradient \(\gamma\)에 대한 정의에 의해 모든 lasso solution \(\hat{\beta}\)에 대해 \(\hat{\beta}_{-\mathcal{E}} = 0\)임을 알 수 있다. 그러므로 (2)를 \(\mathcal{E}\) 블록에 대해 표현하면 다음과 같다.

\[X^T_\mathcal{E} ( y - X_\mathcal{E} \hat{\beta_\mathcal{E}} ) = \lambda \gamma_\mathcal{E}= \lambda s. \qquad \text{ --- (6)}\]

(6)의 양변에 \(X^T_\mathcal{E} (X^T_\mathcal{E})^+\)를 곱하면 다음과 같이 정리된다 (\((X^T_\mathcal{E})^+\)는 \(X^T_\mathcal{E}\)의 pseudoinverse matrix).

\[\begin{align} & X^T_\mathcal{E} X_\mathcal{E} \hat{\beta_\mathcal{E}} = X^T_\mathcal{E} ( y - (X^T_\mathcal{E})^+ \lambda s) \\\\ \Leftrightarrow & X_\mathcal{E} \hat{\beta_\mathcal{E}} = X^T_\mathcal{E} (X^T_\mathcal{E})^+ ( y - (X^T_\mathcal{E})^+ \lambda s). \end{align}\]

\(X\hat{\beta} = X_\mathcal{E} \hat{\beta_\mathcal{E}}\)이므로 위 등식은 곧 아래와 같다.

\[X \hat{\beta} = X^T_\mathcal{E} (X^T_\mathcal{E})^+ ( y - (X^T_\mathcal{E})^+ \lambda s), \qquad \text{ --- (7)}\]

그리고 임의의 lasso solution \(\hat{\beta}\)는 다음과 같다.

\[\begin{align} & \hat{\beta_{-\mathcal{E}}} = 0 \text{ and } \hat{\beta_{\mathcal{E}}} = (X^T_\mathcal{E})^+ ( y - (X^T_\mathcal{E}) + b, \qquad \text{ --- (8)} \\\\ & \text{where } b \in null(X_\mathcal{E}). \end{align}\]

Sufficient conditions for uniqueness

(8)의 \(\hat{\beta_{\mathcal{E}}}\)의 유일함이 보장되기 위해서는 \(b=0\)이 되어야 한다 ( \((X^T_\mathcal{E})^+ ( y - (X^T_\mathcal{E})\)은 유일하기 때문에). \(b=0\)이어야 함을 주지하고 (8)의 등식을 변형하면 다음의 결론을 얻게 된다.

Lemma 2. 임의의 \(y, X, \lambda > 0\)에 대해, 만약 \(null(X_\mathcal{E}) = {0}\), 또는 \(rank(X_\mathcal{E}) = \vert\mathcal{E}\vert\) (참고),이면 lasso solution은 유일(unique)해지며, 이는 곧 다음과도 같다.

\[\begin{align} && \hat{\beta_{-\mathcal{E}}} = 0 \text{ and } \hat{\beta_{\mathcal{E}}} = (X^T_\mathcal{E}X^T_\mathcal{E})^{-1} ( X^T_\mathcal{E} y - \lambda s), \qquad \text{ --- (9)} \\\\ && \text{where } \mathcal{E} \text{ and } s \text{ are the equicorrelation set and signs as defined in (4) and (5)}. \end{align}\]

참고로 이 solution은 많아 봐야 \(min\{n, p\}\)의 nonzero components로 구성된다.

그렇다면 \(null(X_\mathcal{E}) = {0}\)을 암시하는 (\(X\)에 대한) 좀 더 자연스러운 조건에 대해 알아보도록 하자. 이를 알아보기에 앞서 우선 \(null(X_\mathcal{E}) \neq {0}\)이라 가정해보겠다. 이 경우, 어떤 \(i \in \mathcal{E}\)에 대해 다음과 같은 등식을 만족한다.

\[X_i = \sum_{j \in \mathcal{E} \backslash \{i\} } c_j X_j,\\\\ \text{where } c_j \in \mathbb{R}, j \in \mathcal{E}.\]

위 등식의 양변에 \(s_i\)를 곱해주고, 우항에 \(s_j s_j = 1\)을 곱해준다.

\[s_i X_i = \sum_{j \in \mathcal{E} \backslash \{i\} } (s_i s_j c_j) \cdot (s_j X_j). \qquad \text{ --- (10)}\]

\(r = y - X \hat{\beta}\)로 r(lasso residual)을 정의하면 임의의 \(j \in \mathcal{E}\)에 대해 \(X_j^T r = s_j \lambda\)를 만족한다. r을 위 (10)의 양변에 곱해주면 \(\lambda\)에 대한 부등식을 얻을 수 있다. (\(\lambda > 0\)이라 가정)

\[\lambda = \sum_{j \in \mathcal{E} \backslash \{i\} } (s_i s_j c_j) \lambda \quad \text{ and } \quad \sum_{j \in \mathcal{E} \backslash \{i\} } (s_i s_j c_j) = 1.\]

즉, \(null(X_\mathcal{E}) \neq {0}\)이면, 어떤 \(i \in \mathcal{E}\)에 대해 다음 등식이 성립한다.

\[s_iX_i = \sum_{j \in \mathcal{E} \backslash \{i\} } a_j \cdot s_j X_j, \text{ with } \sum_{j \in \mathcal{E} \backslash \{i\} } a_j = 1.\]

위 등식은 \(s_iX_i\)이 \(s_j X_j, j \in \mathcal{E} \backslash \{i\}\)의 affine span 위에 존재한다는 의미와도 같다. 또한 이는 어떤 k+2개의 원소를 포함한 subset으로는 최대 k dimensional affine space만을 표현할 수 있다는 것과도 같다.

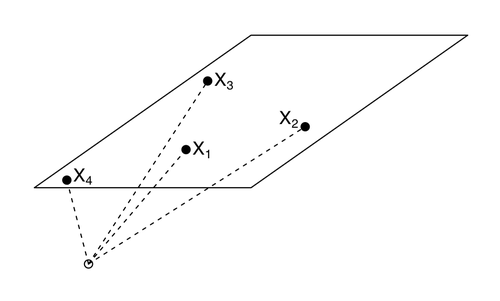
우리가 원하는 것은 행렬 \(X \in \mathbb{R}^{n \text{ x } p}\)가 \(null(X_\mathcal{E}) = {0}\)을 만족하는 것이며, 이는 곧 행렬 \(X\)의 column들이 general position에 있는 것과도 같다. 바꿔말하면, 그 어떤 k-dimensional affine subspace도 set 안의 k+1개보다 더 많은 element를 포함하지 않는다는 것이다.

Lemma 3. 만약 행렬 \(X\)의 column들이 general position에 있으면, 임의의 \(y\)와 \(\lambda > 0\)에 대한 lasso solution은 유일(unique)하며 또한 이 solution은 (9)를 만족한다.

그렇다면 어떤 행렬 \(X\)가 항상 위 조건을 만족할 수 있을까? 결론부터 말하자면 다음과 같다.

Lemma 4. 행렬 \(X \in \mathbb{R}^{n \text{ x } p}\)의 모든 원소가 \(\mathbb{R}^{np}\) 상의 continuous probability distribution을 따른다면, 임의의 \(y\)와 \(\lambda > 0\)에 대해 lasso solution은 unique하고 항상 (9)를 만족한다.

왜냐하면 continuous probability distribution을 따를때, 모든 column vector들은 linearly independent하기 때문이다. (참고)

General convex loss functions

좀 더 일반적인 lasso problem에 대해서도 같은 내용을 적용할 수 있다 [13].

\[\hat{\beta} \in \text{argmin}_{\beta \in \mathbb{R}^p} f(X\beta) + \lambda \|\beta\|_1, \qquad \text{ --- (11) }\]

Lemma 5. 만약 행렬 \(X \in \mathbb{R}^{n \text{ x } p}\)의 모든 원소가 \(\mathbb{R}^{np}\) 상의 continuous probability distribution을 따를때, 미분 가능하고 strictly convex인 임의의 함수 \(f\)는 임의의 \(\lambda > 0\)에 대해 (11)의 문제에서 항상 유일(unique)한 solution을 보장한다. 이 solution은 많아봐야 \(min\{n,p\}\)개의 nonzero components로 구성된다.