12-05 Constrained and Lagrange forms
통계학과 기계학습에서는 종종 constrained form과 Lagrange form 사이를 오가곤 한다. Constrained form과 Lagrangian form을 다음과 같이 정의해보자.
Constrained Form (이하 (C))
\[\min_x \: f(x) \quad \text{ subject to } h(x) \le t,\\\\ \text{where } t \in \mathbb{R} \text{ is a tuning parameter.}\]
Lagrange Form (이하 (L))
\[\min_x \: f(x) + \lambda \cdot h(x),\\\\ \text{where } \lambda \ge 0 \text{ is a tuning parameter.}\]
\(f, h\)가 convex라고 가정할때, 두 문제가 동일한 solution을 도출하는 경우에 대해 알아보도록 하자.
- (C) to (L): (C)가 strictly feasible (Slater’s condition을 만족)하여 strong duality를 만족할 때, (C)의 solution인 \(x^\star\)에 대해 다음의 목적함수를 최소화하는 dual solution \(\lambda^\star \ge 0\)가 존재한다면 \(x^\star\)는 또한 (L)의 solution이다.
- (L) to (C): 만약 \(x^\star\)가 (L)의 solution이고, \(t = h(x^\star)\)인 (C)가 KKT conditions를 만족하면, \(x^\star\)는 또한 (C)의 solution이다. (L)의 KKT conditions를 만족하는 \(\lambda^\star, x^\star\)는 \(t = h(x^\star)\)인 (C)의 KKT conditions를 또한 만족하기 때문이다.
\(\rightarrow\) (L)의 KKT conditions:
\[\begin{align} \nabla_x f(x^\star) + \lambda^\star \nabla_x h(x^\star) &= 0\\\\ \lambda^\star &\ge 0\\\\ \end{align}\]\(\rightarrow\) \(t = h(x^\star)\)인 (C)의 KKT conditions:
\[\begin{align} \nabla_x f(x^\star) + \lambda^\star \nabla_x h(x^\star) &= 0\\\\ \lambda^\star &\ge 0\\\\ \lambda^\star (\underbrace{h(x^\star) - h(x^\star)}_{=0}) &= 0 \end{align}\]
결론적으로 1과 2는 각각 다음과 같은 관계를 보인다.
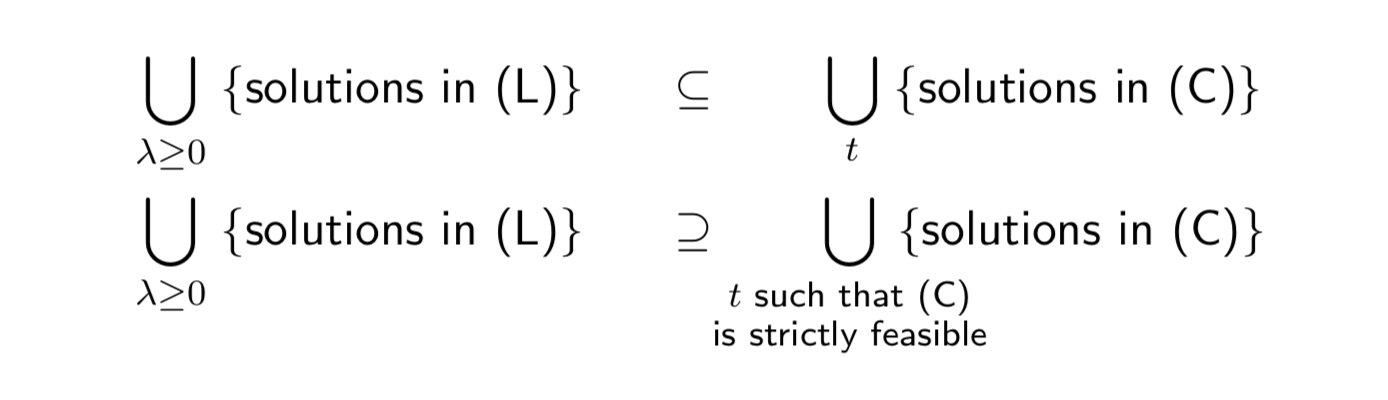
그렇다면 어떤 상황에서 (C)와 (L)이 perfect equivalence를 보이게 될까?
가령, \(h(x) \ge 0\) (예를 들어 norm), \(t = 0\)이고, \(\lambda = \infty\)인 경우에는 perfect equivalence를 보인다. 주어진 조건에 의해 (C)에서의 제약조건은 \(h(x) = 0\)이 되는데, \(\lambda\)를 \(\infty\)으로 설정하게되면 (L)에서 또한 동일한 제약조건(\(h(x) = 0\))을 거는 것과 같은 효과를 보인다.