11-3 Lagrange dual problem

다음과 같이 문제가 주어졌다고 하자.

\[\begin{alignat}{1} \min_x & \quad f(x) \\\\ s.t. & \quad h_i(x) \leq 0, i=1,\dots,m \\\\ & \quad l_j(x) = 0, j=1,\dots,r \end{alignat}\]

Dual function \(g(u,v)\)는 모든 \(u\geq 0\)와 \(v\)에 대해 \(f^* \geq g(u,v)\)를 만족한다. 따라서, 모든 feasible한 \(u\), \(v\)에 대해서 \(g(u,v)\)를 최대화함으로써 가장 좋은 lower bound를 구할 수 있다. 이를 Lagrange dual problem 이라 한다.

\[\begin{alignat}{1} \max_{u,v} & \quad g(u,v) \\\\ s.t. & \quad u \geq 0 \end{alignat}\]

여기서, dual 최적값을 \(g^*\)라고 하면 \(f^* \geq g^*\)이다. 이를 weak duality라 한다. 이 성질은 primal 문제가 convex가 아니어도 항상 성립한다. 또한, dual problem은 primal problem이 convex가 아니더라도 항상 convex optimizaton problem이 된다.

정의에 의해 \(g\)는 \((u,v)\)에 대해 concave 하고, \(u>0\)는 convex 제약조건이다. 따라서, dual 문제는 concave maximization 문제에 해당된다.

\begin{alignat}{1} g(u,v) & = \min_x \{ f(x) + \sum_{i=1}^m u_i h_i(x) + \sum_{j=1}^r v_j l_j(x) \} \\ & = - \underbrace{\max_x \{ -f(x) - \sum_{i=1}^m u_i h_i(x) - \sum_{j=1}^r v_j l_j(x) \}}_{\text{pointwise maximum of convex functions in $(u,v)$}} \end{alignat}

Example: nonconvex quartic minimization

다음 함수 \(f(x)=x^4 - 50 x^2 + 100 x\)를 \(x \geq -4.5\)에 대해 최소화 해 보자.

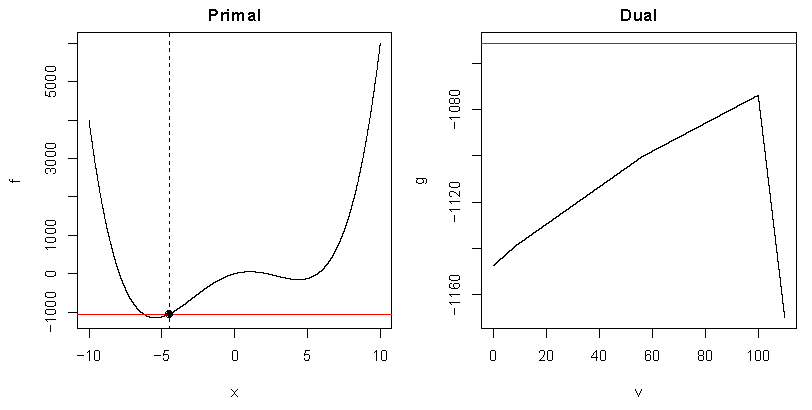
이 때, Dual 함수 \(g\)는 아래와 같다.

\[\begin{equation} g(u) = \min_{i=1,2,3} \{F_i^4(u) - 50 F_i^2(u) + 100 F_i(u) \} \end{equation}\]

여기서, \(i=1,2,3\)에 대해,

\[\begin{alignat}{1} F_i(u) = & \frac{- a_i}{12\cdot 2^{1/3}} \left( 432(100-u)-(432^2(100-u)^2 - 4\cdot 1200^3)^{1/2} \right )^{1/3} \\\\ & - 100 \cdot 2^{1/3} \frac{1}{\left( 432(100-u)-(432^2(100-u)^2 - 4\cdot 1200^3)^{1/2} \right )^{1/3}} \end{alignat}\]

그리고, \(a_1=1, a_2 = (-1+i\sqrt{3})/2, a_3 = (-1-i \sqrt{3})/2\)이다.

함수만 보면 \(g\)가 concave인지 알기어렵지만, duality의 convexity 하에 \(g\)가 concave라는 것을 알 수 있다.