모두를 위한 컨벡스 최적화

11-2 Lagrange dual function

\(C\)를 primal feasible set 이라 하고, \(f^*\)는 primal 최적값이라 하자. 모든 \(x\)에 대해 \(L(x,u,v)\)를 최소화하면 다음과 같은 lower bound를 갖는다.

\[\begin{equation} f^* \geq \min_{x \in C} L(x,u,v) \geq \min_x L(x,u,v) := g(u,v) \end{equation}\]

여기서, \(g(u,v)\)를 Lagrange dual function이라고 하며 임의의 dual feasible \(u\geq 0\), \(v\)에 대해 \(f^*\)의 lower bound를 제공한다.

예를 들면, 아래 그림에서

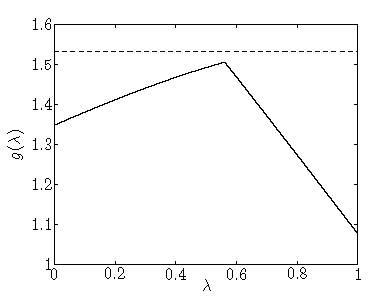
[Fig 2] Example of Lagrangian dual function[1]

  • Dashed horizontal line은 함수 \(f^*\)을 의미
  • Dual 변수는 \(\lambda\)이며
  • Solid line은 \(g(\lambda)\)를 의미

Example: Quadratic Program

1) Positive Definite (\(Q \succ 0\))

다음 quadratic 문제를 가정하자. (여기서 \(Q \succ 0\))

\[\begin{alignat}{1} \min_x & \quad \frac{1}{2}x^T Q x + c^T x \\\\ s.t. & \quad Ax = b, \\\\ & \quad x \geq 0 \end{alignat}\]

그러면,

Lagrangian:
\[\begin{equation} L(x,u,v) = \frac{1}{2}x^T Q x + c^T x - u^Tx + v^T (Ax-b) \end{equation}\]
Lagrangian dual function:

위 식에서, Lagrangian 함수를 최소화하기 위해, \(x\)에 대해서 미분을 해서 미분값이 \(0\)이 되는 \(x^*\)를 찾는다. \begin{equation} Qx - (c-u+A^T v) = 0, \end{equation} 즉, \begin{equation} Qx = (c-u+A^T v) \end{equation} 이 때, \(Q\)는 positive definite하므로 역행렬이 존재하므로, \(x^*\)를 찾으면, \(x^* = Q^{-1}(c - u + A^Tv)\) 임을 알 수 있다. 따라서, \(x^*\)를 Lagrangian 함수에 대입을 하면, 아래를 얻을 수 있다.

\[\begin{alignat}{1} & (c - u + A^T v)^T (Q^{-1})^T Q Q^{-1}(c - u + A^T v) - (c - u + A^T v)^T Q^{-1} (c - u + A^T v) - b^T v \\\ = & (c - u + A^T v)^T Q^{-1}(c - u + A^T v) - (c - u + A^T v)^T Q^{-1} (c - u + A^T v) - b^T v \\\ = & -\frac{1}{2} (c-u+A^Tv)^T Q^{-1} (c-u+A^T v) - b^T v \end{alignat}\]

따라서,

\[\begin{equation} g(u,v) = \min_x L(x,u,v) = -\frac{1}{2} (c-u+A^Tv)^T Q^{-1} (c-u+A^T v) - b^T v \end{equation}\]

모든 \(u \geq 0\)과 \(v\)에 대해, 이것은 primal 최적값 \(f^*\)에 대한 lower bound에 해당된다.

2) Positive Semidefinite (\(Q \succeq 0\))

위와 같은문제이나, 이번에는 \(Q \succeq 0\) 이면,

Lagrangian:
\[\begin{equation} L(x,u,v) = \frac{1}{2}x^T Q x + c^T x - u^Tx + v^T (Ax-b) \end{equation}\]
Lagrangian dual function:

\(Q\)가 positive definite 할 때 처럼, 아래 식을 만족하는 \(x^*\)를 찾아야 한다.

\(\begin{equation} Qx = (c-u+A^T v) \end{equation}\) 이 때, \(Q\)는 positive semi-definite이므로 역행렬이 존재하지 않을 수 있다. 따라서, 다음의 두가지 경우를 고려해야 한다.

(1) \(c-u+A^T v \in col(Q)\). 이 경우는 위 \(Qx = (c-u+A^T v)\)를 만족시키는 \(x^*\)가 존재하는 것을 의미하며, 이는 generalized inverse \(Q^+\)를 이용하여 찾을 수 있다. (참고로, generalized inverse는 Moore-Penrose Pseudo Inverse로 \(Q^+ = (Q^TQ)^{-1}Q^T)\)이다.)

(2) \(c-u+A^T v \notin col(Q)\). 이 경우는 위 \(Qx = (c-u+A^T v)\)를 만족시키는 \(x^*\)가 존재하지 않는 것을 의미하며, 즉 \(L(x,u,v)\)가 최소값을 갖도록 하는 \(x^*\)를 갖지 않는 다는 것은 \(L(x,u,v)\)의 최소값이 \(-\infty\)임을 의미함.

위 두 경우로부터, Lagrangian dual function을 아래와 같이 정리할 수 있다.

\[g(u,v) = \begin{cases} -\frac{1}{2} (c-u+A^T v)^T Q^{+} (c - u + A^T v) - b^T v & \text{if $c-u+A^T v \perp \text{null}(Q)$} \\\\ -\infty & \text{otherwise} \end{cases}\]

모든 \(u\geq 0\), \(v\), \(c-u+A^Tv \perp \text{null}(Q)\)에 대해서, \(g(u,v)\)는 \(f^*\)에 대한 nontrivial lower bound 이다.

Example: Quadratic Program in 2D

예를 들면, 아래 그림에서 \(f(x_1,x_2)\)는 0보다 큰 값들을 변수(\(x\ge0\))로 갖는 이차함수이며, dual 함수 \(g(u_1,u_2)\)는 0보다 큰 값을 변수(\(u\ge0\))로 갖는 이차함수이다

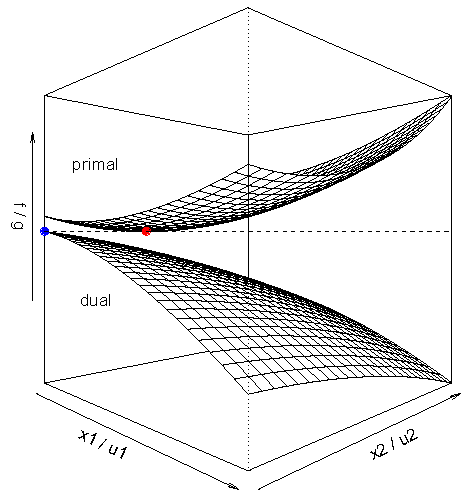
[Fig 3] Example of quadratic program in 2D

  • 파란점은 최적 dual value 이고, 빨간점은 최적 primal value 이다.
  • Dual 함수 \(g(u)\)는 0보다 큰 모든 \(u\)에 대해서, \(f^*\)에 대한 lower bound를 제공한다.
  • Dual 함수 \(g(u)\)의 가장 큰 값이 정확히 \(f^*\)값과 일치함을 보인다.