11-1 Lagrangian

다음은 다음 최적화 문제에 대한 Lagrangian 형태를 살펴본다. 여기서, 최적화 문제는 반드시 convex일 필요는 없다.

\[\begin{alignat}{1} \min_x & \quad f(x) \\\ s.t. & \quad h_i(x) \leq 0, i = 1,\dots,m \\\ & \quad l_j(x) = 0, j=1,\dots,r \end{alignat}\]

이 때, Lagrangian은 아래와 같이 정의한다.

\[\begin{equation} L(x,u,v) = f(x) + \sum_{i=1}^m u_i h_i(x) + \sum_{j=1}^r v_j l_j(x) \end{equation}\]

여기서, \(u \in \mathbb{R}^m\), \(v \in \mathbb{R}^r\), \(u \geq 0\) (implicitly, \(L(x,u,v) = - \infty\) for \(u <0\)).

위 Lagrangian에서, \(h_i(x) \leq 0\), \(l_j(x)=0\) 이므로,

\[\begin{equation} L(x,u,v) = f(x) + \sum_{i=1}^{m} u_i \underbrace{h_i(x)}_{\leq 0} + \sum_{j=1}^r v_j \underbrace{l_j(x)}_{=0} \leq f(x) \end{equation}\]

즉, Lagrangian은 다음의 중요한 성질을 갖는다.

모든, \(u \geq 0\), \(v\)에 대해, \(f(x) \geq L(x,u,v) \text{ at each feasible $x$}\)

예를 들면, 아래 그림에서,

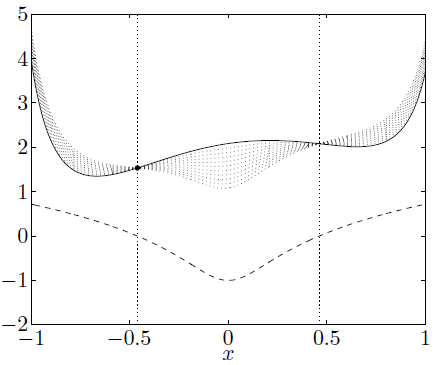
• Solid line은 함수 \(f\)를 의미
• Dashed line은 함수 \(h\)를 의미함. 여기서 feasible set 대략 \([-0.46,0.46]\)임
• 각 Dotted line은 \(u \geq 0\), \(v\)에 대한 함수 \(L(x,u,v)\)를 의미