09-05-03 Example : FISTA

Example : FISTA

이 절에서는 Accelerated proximal gradient method의 예제로서 FISTA를 살펴볼 것이다. FISTA는 ISTA(Iterative Soft-thresholding Algorithm)의 accerated version이라고 할 수 있다.

FISTA (Fast Iterative Shrinkage-thresholding Algorithm)

이전에 정의했던 Lasso problem을 기억해보자. \(y \in \mathbb{R}^n\), \(X \in \mathbb{R}^{n \times p}\)일 때, lasso criterion은 다음과 같이 정의되었다.

\[\min_\beta \frac{1}{2} \lVert y−X\beta \rVert_2^2 + \lambda \lVert \beta \rVert_1\]

그리고, ISTA의 정의도 기억해 보자. \(S_\lambda (·)\)는 vector soft-thresholding일 떄 Proximal gradient update가 다음과 같이 정의되었었다. (09-01 Proximal gradient descent 참조)

\[\beta^{(k)} = S_{\lambda t_k} (\beta^{(k−1)} + t_kX^T(y − X\beta^{(k−1)})), k = 1,2,3,...\]

이 식에 acceleration을 적용하면 \(\beta\) 대신에 \(v\)를 계산해서 proximal gradient update를 한다.

\[v = \beta^{(k−1)} + \frac{k − 2}{k + 1} (\beta^{(k−1)} − \beta^{(k−2)}) \\ β(k) = S_{\lambda t_k} (v + t_kX^T(y−Xv) ), k = 1,2,3,...,\]

다음 그림은 lasso regression에 FISTA를 적용한 결과로 100개의 instance에 대해 실행하였다.

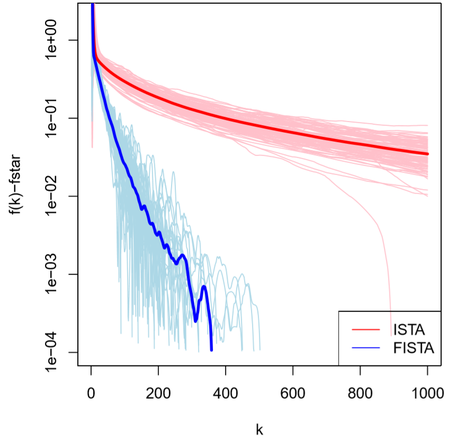
다음 그림은 lasso logistic regression에 FISTA를 적용한 결과이다.

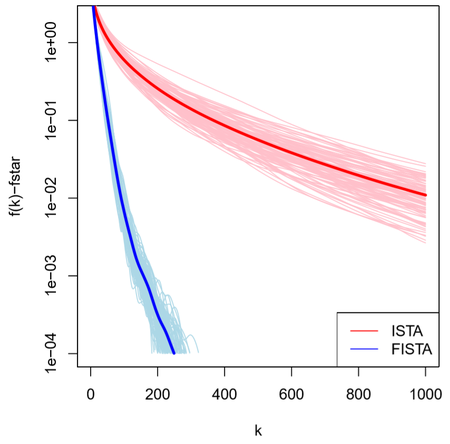
100가지의 샘플을 토대로 Lasso regression, lasso logistic regression 에 대해 평균을 낸 결과, \(k\)값이 증가할수록 FISTA 기법이 훨씬 더 빠르게 수렴하는 것을 확인할 수 있다.