09-01 Proximal gradient descent

Proximal gradient descent

Proximal gradient descent는 objective 함수를 differentiable한 함수와 non-differentiable한 함수로 분리해서 최적해를 찾는 방법이다. 이 절에서는 proximal gradient descent에서 함수를 정의하는 방식과 최적해를 구하는 방식을 살펴보도록 하겠다.

Decomposable functions

Objective 함수 \(f\)를 두 개의 함수 \(g\)와 \(h\)로 분리할 수 있다고 가정하자.

\[f(x) = g(x) + h(x)\]

이때, 두 함수 함수 \(g\)와 \(h\)는 다음과 같은 성질을 갖는다.

• \(g\)는 convex이고 differentiable하다. (dom\((g) = \mathbb{R}^n\))
• \(h\)는 convex이고 non-differentiable하다.

만일 \(f\)가 differentiable하다면 gradient descent로 다음 위치를 찾을 수 있을 것이다.

\[x^+ = x - t \cdot \nabla f(x)\]

[참고] Gradient descent에서는 함수 \(f\)를 \(x\) 근처에서 Taylor 2차식으로 근사하고 2차 항의 hessian \(\nabla^2 f(x)\)를 \(\frac{1}{2t} I\)로 대체해서 정의한다. 그리고, 이 근사식의 최소 위치를 다음 위치로 선정한다. (자세한 내용은 6장 Gradient descent 참조)

\begin{align} x^+ = \underset{z}{\text{argmin}} \underbrace{ f(x) + \nabla f(x)^T (z - x) + \frac{1}{2t} \parallel z - x \parallel_2 ^2}_{\tilde{f}_t(z)} \end{align}

하지만, 함수 \(f\)가 differentiable하지 않다면 gradient descent를 사용할 수 없다. 그런데, 함수 \(f\)가 \(f = g + h\)로 구성된다면 differentiable한 함수 \(g\)는 이차식으로 근사할 수 있지 않을까?

이런 아이디어에서 나온 방법이 Proximal gradient descent이다. 이 방법에서는 \(g\)의 gradient descent로 예측된 위치와 가까우면서 non-differentiable한 함수 \(h\)를 동시에 작아지게 만들 수 있는 가장 좋은 위치로 조정하는 방식이다. 이런 과정은 다음 식과 같이 표현될 수 있다.

\[\begin{align} x^+ & = \underset{z}{\text{argmin}} \tilde{g}_t(z) + h(z) \\ & = \underset{z}{\text{argmin}} \ g(x) + \nabla g(x)^T (z - x) + \frac{1}{2t} \parallel z - x \parallel_2 ^2 + h(z) \\ & = \underset{z}{\text{argmin}} \nabla g(x)^T (z - x) + \frac{1}{2t} \parallel z - x \parallel_2 ^2 + \frac{t}{2} \parallel \nabla g(x) \parallel_2 ^2 + h(z) \\ & = \underset{z}{\text{argmin}} \frac{1}{2t} \left ( 2t \nabla g(x)^T (z - x) + \parallel z - x \parallel_2 ^2 + t^2 \parallel \nabla g(x) \parallel_2 ^2 \right ) + h(z) \\ & = \underset{z}{\text{argmin}} \frac{1}{2t} \left ( \parallel z - x \parallel_2 ^2 + 2t \nabla g(x)^T (z - x) + t^2 \parallel \nabla g(x) \parallel_2 ^2 \right ) + h(z) \\ & = \underset{z}{\text{argmin}} \frac{1}{2t} \parallel z - (x - t \nabla g(x) )\parallel_2 ^2 + h(z) \\ \end{align}\]

2줄에서 3줄로 갈 때 z에 대한 상수항으로서 \(g(x)\)는 삭제되고 \(\frac{t}{2} \parallel \nabla g(x)^T \parallel_2 ^2\) 항이 추가되었다. 최종 식에서 첫번째 항 \(\frac{1}{2t} \parallel z - (x - t \nabla g(x) )\parallel_2 ^2\)은 \(g\)의 gradient update 위치에 가까워지게 만드는 항이고 두번째 항인 \(h(z)\)는 \(h\)를 작아지게 만드는 항이다.

Proximal gradient descent

Proximal gradient descent는 시작점 \(x^{(0)}\)에서 시작해서 다음 과정을 반복한다.

\(x^{(k)} = \text{prox}_{t_k}(x^{(k-1)} - t_k \nabla g(x^{(k-1)}) )\), \(k=1,2,3,...\)

여기서 \(\text{prox}_{t}\)는 proximal mapping으로 다음과 같이 정의된다.

\begin{align} \text{prox}_{t}(x) = \underset{z}{\arg \min} \frac{1}{2t} \parallel x - z \parallel_2^2 + h(z) \end{align}

이 식을 그동안 봐왔던 update 형태로 변경해 보면 다음과 같다. 여기서 \(G_{t}\)는 \(f\)의 generalized gradient이다.

\begin{align} x^{(k)} = x^{(k-1)} - t_k \cdot G_{t_k}(x^{(k-1)}), \space \space \text{where} \space G_{t}(x) = \frac{x-\text{prox}_{t} (x - t \nabla g(x))}{t}
\end{align}

What good did this do?

이렇게 하면 무엇이 좋아지는가? 단지 문제를 다른 형태의 minimization 문제로 바꾼 것이 불과하지 않은가?라고 의문을 가질 수 있다.

핵심 포인트는 대부분의 주요 \(h\) 함수에 대해 \(\text{prox}_{t}(\cdot)\)가 분석적으로 계산될 수 있다는 것이다. 즉, 다음과 같이 계산된다.

• 맵핑 함수 \(\text{prox}_{t}(\cdot)\)는 \(g\)가 아닌 \(h\)에만 의존한다.
• 함수 \(g\)는 매우 복잡한 함수일 수 있는데 여기서는 gradient \(\nabla g\)만 계산하면 된다.

수렴 분석은 알고리즘의 반복 횟수에 대해 이뤄지게 될 것이다. 각 반복에서 \(\text{prox}_{t}(\cdot)\)를 계산하며 \(h\)에 따라 계산 비용이 작거나 커질 수 있다는 점을 유의해야 한다.

Example: ISTA

Proximal gradient descent의 예제를 살펴보자. 이전 장에서 \(y \in \mathbb{R}^n\), \(X \in \mathbb{R}^{n \times p}\)일 때, lasso criterion은 다음과 같이 정의되었다.

\begin{align} f(\beta) = \frac{1}{2} \parallel y - X\beta \parallel_2^2 + \lambda \parallel \beta \parallel_1
\end{align}

여기서 \(g(\beta) = \frac{1}{2} \parallel y - X\beta \parallel_2^2\)이고 \(h(\beta) = \lambda \parallel \beta \parallel_1\)이다. 이때, proximal mapping은 다음과 같이 정의된다.

\[\begin{align} \text{prox}_{t}(\beta) & = \underset{z}{\text{argmin}} \frac{1}{2t} \parallel \beta - z \parallel_2^2 + \lambda \parallel z \parallel_1 \\ & = S_{\lambda t}(\beta) \\ \end{align}\]

\(S_{\lambda t}(\beta)\)는 soft-thresholding operator로 다음과 같이 정의된다. (자세한 내용은 7장 Subgradient 참조)

\[\begin{align} [S_{\lambda t}(\beta)]_i = \begin{cases} \beta_i - \lambda & \mbox{if } \beta_i \gt \lambda \\ 0 & \mbox{if } \lambda \le \beta_i \le \lambda, i = 1, ..., n \\ \beta_i + \lambda & \mbox{if } \beta_i \lt -\lambda \\ \end{cases} \\ \end{align}\]

\(g\)의 gradient가 \(\nabla g(\beta) = -X^{T} (y - X \beta)\)이므로 proximal gradient update는 다음과 같이 정의된다.

\[\beta^+ = S_{\lambda t}(\beta + tX^{T} (y - X \beta) )\]

이 알고리즘은 iterative soft-thresholding algorithm (ISTA) 라고 하는 매우 간단한 알고리즘이다. (Beck and Teboulle (2008), “A fast iterative shrinkage-thresholding algorithm for linear inverse problems”)

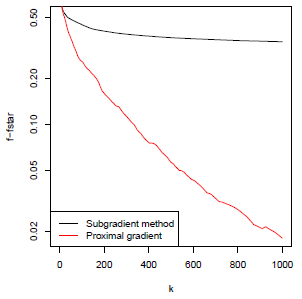
다음 그림을 보면 subgradient method와 proximal gradient descent의 확연한 성능 차이를 확인할 수 있다. 반복 횟수 측면에서 proximal gradient descent의 성능은 gradient cescent의 성능과 동일하다.