06-02-01 Fixed step size

Gradient decent에서 step size를 찾는 가장 단순한 방법은 모든 반복에서 t를 고정하는 것이다. 하지만 step size \(t_k = t\), \(k = 1, 2, 3, ...\)의 크기에 따라 수렴할 수도 있으고 발산할 수도 있다.

예를 들어 아래 그림을 보면 함수 \(f(x) = (10 x_1^2 + x_2^2) / 2\)에 대해 gradient descent를 수행을 보여주고 있다.

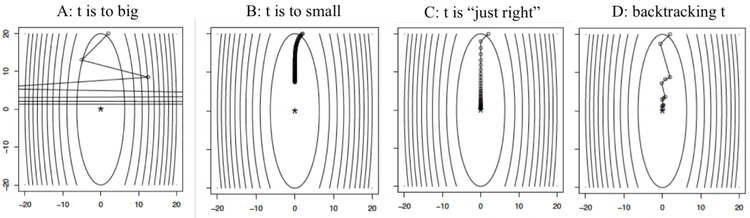
• A의 경우 step size \(t\)가 매우 큰 경우로 8 step 이후 발산하였다. 이 경우 절대로 minimum값에 도달할 수 없다.
• 반면 그림 B와 같이 step size \(t\)가 아주 작으면 수렴의 속도가 매우 느려져서 100 step에서도 수렴하지 못한다. 즉, 최소에 가까워질수록 \(\nabla f(x)\)가 0에 가까워지므로 step \(t \nabla f(x)\)도 아주 작아져서 진행이 점점 느려지게 된다.
• (시행착오에 의해 발견한) \(t\)값이 “적절한 값”이라면 C와 같이 잘 수렴하게 된다. 이 때는 40 정도 진행한 상황이다. (이 “적절한 값”은 수렴 분석을 통해 찾을 수 있으며 이 장의 뒷부분에서 소개한다.)