03-04-02 Basic properties

Quasiconvex는 convex function의 일반화라는 것을 앞 절의 예에서 살펴보았다. 이런 관점에서, 이 절에서는 convex function에서의 성질이 quasiconvex function에서도 유지되는지에 관하여 살펴본다.

Modified Jensen’s inequality

Quasiconvex는 Jensen’s inequality 를 통해 다음과 같이 정의된다.

\(f(\theta x + (1 - \theta)y) \leq \max\{f(x), f(y)\}\) for all \(x, y \in \text{dom}f, 0 \leq \theta \leq 1\)

아래 그림은 함수 \(f\)가 quasiconvex 이면, 두 점에서 그은 선분 사이의 \(f\)값이 각 끝점에서의 \(f\)의 maximum을 넘지 않는다는 것을 보여준다.

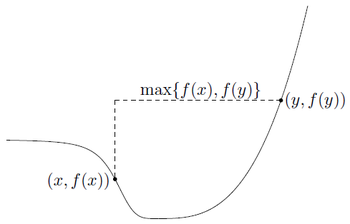
quasiconvex function on \(\mathbb{R}\). x와 y 사이의 f값은 \(\max\{f(x), f(y)\}\) 보다 작다.

Quasiconvex function on \(\mathbb{R}\)

연속함수 \(f : \mathbb{R} \mapsto \mathbb{R}\)가 quasiconvex라는 것은 다음과 같은 조건 중 적어도 하나를 만족한다는 것을 의미한다.

• \(f\) is nondecreasing
• \(f\) is nonincreasing
• 도메인 상의 특정 한 점, \(c \in \text{dom} f\)을 기준으로, \(t \leq c(t \in \text{dom}f)\)에 대해서, \(f\)는 nonincreasing하고, \(t \geq c(t \in \text{dom}f)\)에 대해서 \(f\)는 nondecreasing하다.

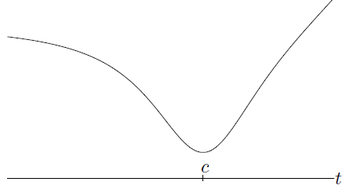
quasiconvex function on \(\mathbb{R}\). \(t leq c(t \in \text{dom} f)\)에서는 nonincreasing, \(t \geq c(t \in \text{dom} f)\)에서는 nondecreasing 하다.