03-04-03 Differentiable quasiconvex functions

Quasiconvex function이 미분가능할 때, First-order conditions, Second-order conditions을 만족하게 된다. 다음을 살펴보자.

First-order conditions

\(f : R^n \rightarrow R\)가 미분 가능 함수라고 하자. \(dom\) \(f\)가 convex 이고, 다음 조건을 만족하면 \(f\)는 quasiconvex 이다.

\(f\) is quasiconvex \(\Longleftrightarrow\) \(f(y) \preceq f(x) , \nabla f(x)^T(y-x) \leq 0.\) for all \(x, y \in dom\) \(f\)

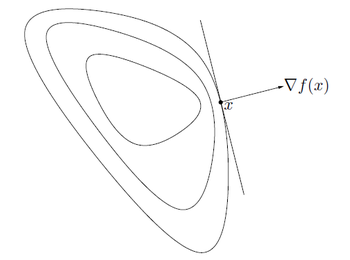
quasiconvex function f 안에서 3개의 level curve를 보여준다. \(\nabla f(x)\)는 \(x\)에서의 sublevel set {\(z \mid f(z) \leq f(x)\)}의 supporting hyperplane을 정의하는 normal vector가 된다.

Quasiconvexity의 First-order condition이 convexity의 First-order characterization (03-01-03 참조)과 유사해 보이지만, 중요한 차이가 존재한다. 예를 들면, \(f\)가 convex이고, \(\nabla f(x) = 0\)이라면, \(x\)는 \(f\)의 global minimizer라는 것이 성립하지만, quasiconvex function에서는 항상 성립하지 않는다.

Second-order conditions

\(f\)가 두번 미분 가능할 때, Second-order conditions가 적용된다. 만약 \(f\)가 quasiconvex라면, 모든 \(x \in dom\) \(f\) 그리고 모든 \(y \in R^n\)에 대하여, 다음 식이 성립한다.

\(f\) is quasiconvex, \(y^T \nabla f(x) = 0 \Longrightarrow y^T \nabla^2 f(x)y \geq 0\) for all \(x \in dom\) \(f\), all \(y \in R^n\)

\(R\)에서 quasiconvex일 때,

\(f\) is quasiconvex, \(f'(x) = 0 \Longrightarrow f''(x) \geq 0\)

즉, zero slope를 갖는 임의의 포인트가 존재한다면, 2차 미분 값은 non-negative가 된다. 다시 \(R^n\)으로 돌아와서, Second-order condition은 다음과 같은 성질 또한 만족한다.

1) \(\nabla f(x) = 0\)일 때, 항상 \(\nabla^2f(x) \succeq 0\)이 만족되어야 한다.
2) \(\nabla f(x) \neq 0\)이라면, \(y^T \nabla f(x) = 0 \Longrightarrow y^T \nabla^2 f(x)y \geq 0\) 에서 \(\nabla^2 f(x)\) 가 헤시안 행렬로 작용하여, \((n\)-\(1)\)-\(dimensional\) \(subspace \nabla f(x)^\perp\)에서 positive semidefinite이 된다.

(\((n\)-\(1)\)-\(dimensional\) \(subspace \nabla f(x)^\perp\)은 \(\nabla f(x)\)와 직교하는 (n-1) 차원의 subspace를 의미한다. (n-1)차원인 이유는 \(\nabla f(x)\)가 n차원 함수 \(f\)를 미분했기 떄문에 차원이 하나 줄었기 때문이다.)