모두를 위한 컨벡스 최적화

17-04 Special case, linear programming

이 절에서는 LP(linear programming) 문제에 대한 Primer-Dual method의 예시를 살펴보자.

Linear programming

다음과 같은 primal LP 문제가 있다.

\[\begin{align} &\min_{x} && {c^Tx} \\\\ &\text{subject to } && {Ax = b} \\\\ & &&{x ≥ 0} \\\ \end{align}\] \[\text{for } c ∈R^n, A ∈R^{m×n}, b ∈R^m\]

위 primal LP 문제의 dual 문제는 아래와 같다.

\[\begin{align} &\max_{y,s} && {b^Ty} \\\\ &\text{subject to } && {A^Ty + s = c} \\\\ & &&{s ≥ 0} \\\ \end{align}\]

Optimality conditions and central path equations

다음은 이전 LP의 primal-dual problem에 대한 최적 조건(KKT Conditions)을 보여준다.

\[\begin{array}{rcl} A^Ty + s & = & c \\\ Ax & = & b \\\ XS\mathbb{1} & = & 0 \\\ x,s & \succeq & 0 \end{array}\]

Central path equations

\[\begin{array}{rcl} A^Ty + s & = & c \\\ Ax & = & b \\\ XS\mathbb{1} & = & τ\mathbb{1} \\\ x,s & > & 0 \end{array}\]

Primal-dual method vs. barrier method

Newton steps for primer-dual method

다음은 LP문제에 대한 primal-dual method의 Newton 방정식이다.

\[\begin{bmatrix} 0 & A^T & I \\\ A & 0 & 0 \\\ S & 0 & X \end{bmatrix} \begin{bmatrix} ∆x \\\ ∆y \\\ ∆s \end{bmatrix}= − \begin{bmatrix} A^Ty + s−c \\\ Ax−b \\\ XS\mathbb{1}−τ\mathbb{1} \end{bmatrix}\]

Optimal condition에서 다음 관계를 알 수 있다.

\[XS\mathbb{1} = \tau \mathbb{1} \iff s = \tau X^{−1}\mathbb{1} \iff x = \tau S^{−1}\mathbb{1}\]

이에 따라 \(s\)를 제거하여 primal barrier problem에 대한 최적 조건을 얻거나, \(x\)를 제거하여 dual barrier problem에 대한 최적 조건을 얻을 수 있다.

Newton steps for barrier problems

다음은 barrier problem에 대한 primal과 dual central path equation이다. (왼쪽이 primal 오른쪽이 dual)

\[\begin{array}{rcr} A^Ty + τX^{−1}1 & = & c & \qquad \qquad & A^Ty + s & = & c \\\ Ax & = & b & \qquad \qquad & τAS^{−1}\mathbb{1} & = & b\\\ x & > & 0 & \qquad \qquad & s & > & 0 \end{array}\]

위의 central path equation으로 primal과 dual에 대한 Newton step을 구해보면 다음과 같다.

Primal Newton step

\[\begin{bmatrix} τX^{−2} & A^T \\\ A & 0 \end{bmatrix} \begin{bmatrix} ∆x \\\ ∆y \end{bmatrix}= − \begin{bmatrix} A^Ty + τX^{−1}\mathbb{1}−c \\\ Ax−b \end{bmatrix}\]

Dual Newton step

\[\begin{bmatrix} A^T & I \\\ 0 & τAS^{−2} \end{bmatrix} \begin{bmatrix} ∆y \\\ ∆s \end{bmatrix}= − \begin{bmatrix} A^Ty + s −c \\\ τAS^{−1}\mathbb{1}−b \end{bmatrix}\]

Example: barrier versus primal-dual

Standard LP : \(n = 50\), \(m = 100\)

Primal-dual method의 성능을 확인하기 위해 변수가 \(n = 50\)이고 equality constraint가 \(m = 100\)인 표준 LP문제에 대한 예시를 살펴보자. (Example from B & V 11.3.2 and 11.7.4)

Barrier method는 다양한 \(\mu\)값(2, 50, 150)을 사용한 반면 primal-dual method에서는 \(\mu\)를 10으로 고정하였다. 그리고 두 방법 모두 \(\alpha = 0.01, \beta = 0.5\)를 사용했다.

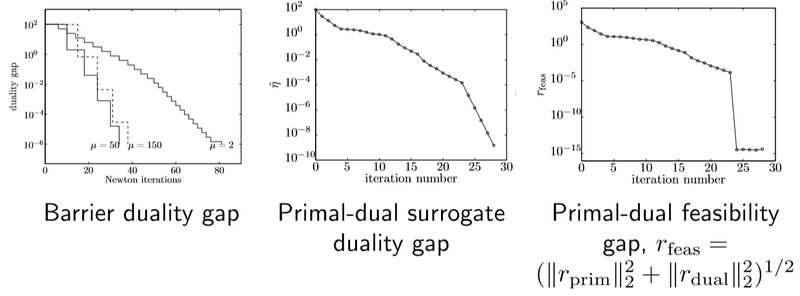
[Fig1] Duality gap (Barrier vs. Primal-dual) [1]

그래프에서 보다시피 primal-dual은 빠르게 수렴하면서도 높은 정확도를 보인다.

Sequence of problem : \(n = 2m\) and \(n\) growing.

이제 \(n = 2m\)이고 \(n\)이 점점 증가하는 일련의 문제에 대해 성능을 살펴보자.

  • Barrier method는 \(\mu = 100\)를 사용하였고 outer loop는 2회 정도만 수행되었다. (duality gap은 \(10^4\)로 감소하였다)
  • Primal-dual method는 \(\mu = 10\)를 사용하였고 duality gap과 feasibility gap이 거의 \(10^{−8}\)일 때 실행을 중단했다.

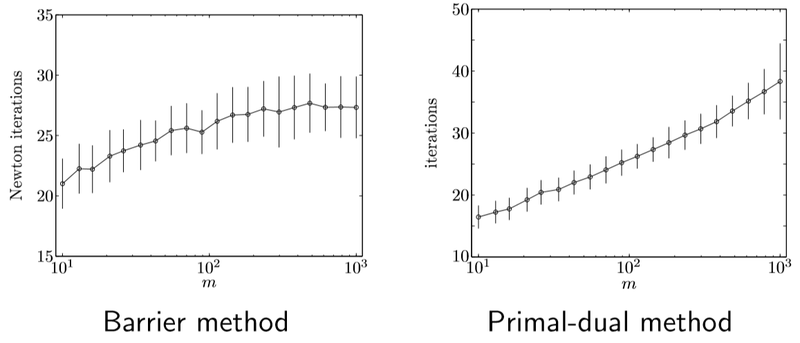
[Fig2] Newton iteration (Barrier vs. Primal-dual) [1]

위 그림에서 알 수 있듯이 Primal-dual 방법은 더 높은 정확도를 갖는 솔루션 찾지만 약간의 iteration이 추가적으로 필요하다.