15-06 Barrier method v.2

이전 알고리즘에서는 central path에 있는 solution을 생성했는데, 실제 centeral path는 optimal로 가는 과정(“means to an end”)일 뿐이다. 따라서, 문제를 정확히 풀 필요는 없다.

Barrier method v.2

이런 이유로 Barrier method v.2은 barrier problem을 approximation해서 풀게 된다.

Algorithm

알고리즘의 단계는 Barrier method v.1과 동일하다.

단, 단계 2의 \(x^{(0)} \approx x^*(t)\)와 단계 3-2의 \(x^{(k+1)} \approx x^*(t)\) 부분이 approximation으로 바뀌었다.

1. \(t^{(0)} \gt 0\)이고 \(k := 0\)을 선택한다.
2. \(t = t^{(0)}\)에서 barrier problem을 풀어서 \(x^{(0)} \approx x^*(t)\)을 구한다.
3. While \(m/t \gt \epsilon\)
   3-1. \(t^{(k+1)} \gt t^{(k)}\)를 선택한다.
   3-2. Newton’s method를 \(x^{(k)}\)로 초기화한다. (warm start)
   \(t = t^{(k+1)}\)에서 barrier problem을 풀어서 \(x^{(k+1)} \approx x^*(t)\)을 구한다.
   end while
   

Important issues (can be formalized):

Barrier method v.2에서는 다음 두 가지 사항이 매우 중요하다.

• 얼마나 근사를 잘 할 수 있는가? (How close should each approximation be?)
• Centering step 별로 얼마나 많은 newton step이 필요한가? (How many Newton steps suffice at each centering step?)

Example of LP

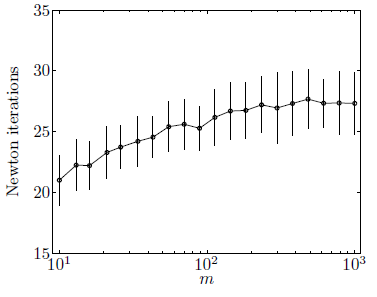
다음 그림을 보면 \(m\)개 constraint를 갖는 문제에 대해 barrier method를 실행해 보면 \(m\)의 크기가 커지더라도 linear convergence를 한다는 것을 볼 수 있다. 즉, \(m\)에 대해 log scale을 갖는다.

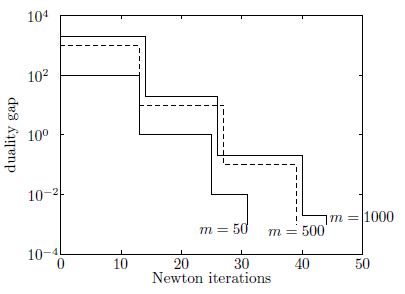
다르게 보면 (\(10^4\)인 초기 suboptimal gap (duality gap)을 줄이기 위해 필요한) newton step은 \(m\)에 대해 천천히 증가한다. 아래 그림을 보면 \(m\)이 크게 증하하더라도 각 centering step 별로 20~30 newton step 정도만 필요하다. 단, 한 newton step은 문제의 크기에 따라 크게 달라진다.