15-04 Barrier method v.0 and v.1
Barrier method v.0
Barrier method v.0은 \(\epsilon \gt 0\)일 때 \(t = m/\epsilon\)로 선택해서 다음 barrier problem을 풀어서 \(f(x^*(t)) - f(x^*) \le \epsilon\)를 구한다.
\[\begin{align} &\min_{x} \ && tf(x) + \phi(x) \\ &\text{subject to } \ && Ax = b \\ \end{align}\]
이때, \(m\)은 constraint개수이고 \(t\)는 \(1/\epsilon\)의 배수이기 때문에 \(\epsilon\)이 작을 수록 \(t\)가 매우 커지게 되며 결국 central path의 끝부분이 되므로 문제는 original problem과 같아진다. 따라서, 매우 느리고 구하기 힘든 문제가 될 수 있다.
따라서, central path를 따라 solution을 구하는 것이 더 나은 방법으로 barrier method v.1이 정의될 수 있다.
Barrier method v.1
Barrier method v.1은 \(t\) 값을 증가시키면서 다음의 barrier problem을 점진적으로 여러번 푸는 방법이다.
\[\begin{align} &\min_{x} \ && tf(x) + \phi(x) \\ &\text{subject to } \ && Ax = b \\ \end{align}\]
Algorithm
알고리즘을 설명하면 다음과 같다.
- \(t^{(0)} \gt 0\)이고 \(k := 0\)을 선택한다.
- \(t = t^{(0)}\)에서 barrier problem을 풀어서 \(x^{(0)} = x^*(t)\)을 구한다.
- While \(m/t \gt \epsilon\)
3-1. \(t^{(k+1)} \gt t^{(k)}\)를 선택한다.
3-2. Newton’s method를 \(x^{(k)}\)로 초기화한다. (warm start)
\(t = t^{(k+1)}\)에서 barrier problem을 풀어서 \(x^{(k+1)} = x^*(t)\)을 구한다.
end while
Comments
- Common update 방법 : \(t^{(k+1)} = \mu t^{(k)}\), (\(\mu \gt 1\))
- Warm start : 단계 3-2에서는 이전 단계의 solution을 다음 단계의 초기값으로 사용하는데 이를 warm start라고 한다.
- Centering step : 알고리즘에서 barrier problem을 푸는 단계인 2와 3-2를 centering step ( or outer iteration)이라고 한다.
Considerations
\(\mu\)와 \(t^{(0)}\)의 선택에 있어서, 다음의 trade off를 고려해야 한다.
\(\mu\)의 선택
- \(\mu\)가 너무 작다면, outer iteration이 많아진다. (이 경우 warm start가 도움이 된다.)
- \(\mu\)가 너무 크다면, 모든 centering step에서 newton method가 수렴할 때까지 iteration을 많이 해야 한다.
알고리즘 초기값 선택
- \(t^{(0)}\)가 너무 작다면, outer iteration이 많아진다.
- \(t^{(0)}\)가 너무 크다면, v.0과 같은 문제가 된다. 따라서, 첫번째 centering step에서 newton method가 \(x^{(0)}\)을 구하기 위해 iteration을 많이 해야 한다.
다행히도 실제 barrier method의 성능은 \(\mu\)와 \(t^{(0)}\)의 선택에 매우 robust한 편이다. 그리고, 이들 parameter의 적절한 범위는 문제의 크기에 따라 달라진다.
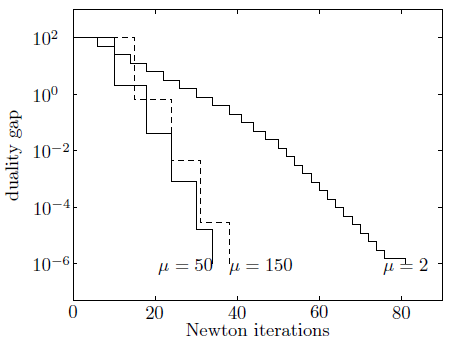
Example of small LP
다음 그릠에는 n=50 dimensions, m=100 inequality constraints 조건의 LP 문제를 barrier method로 실행했을 때 성능을 보여주고 있다. \(\mu = 2\)인 경우 outer iteration이 커지고 \(\mu=150\)인 경우에 centering step이 \(\mu=50\)일 때보다 상대적으로 증가했음을 확인할 수 있다.