15-02 Central path

다음과 같은 barrier problem (\(t \gt 0\))의 solution을 \(x^*(t)\)라고 하면 central path는 set \(\{x^*(t) \vert t \gt 0 \}\)을 말한다.

\[\begin{align} &\min_{x} \ && tf(x) + \phi(x) \\ &\text{subject to } \ && Ax = b \\ \end{align}\]

적합한 조건이 주어지면 central path 집합은 \(\mathbb{R}^n\)에서 smooth path가 되며 \(t \to \infty\)일 때 \(x^*(t) \to x^*\)가 된다. (\(x^*\)는 원래 문제의 solution이다.)

Central path는 boundary에 있는 optimal을 한번에 구하기 어려울 때 interior에서 boundary쪽으로 점진적으로 새로운 \(t\)에 대한 문제로 재정의해서 풀어나가게 되는데, 이 때 각 단계의 해가 이루는 집합이라고 볼 수 있다.

Example : central path for an LP

다음의 LP 문제에 대한 central path를 구해보자.

\[\begin{align*} &\min_{x} \ && c^Tx \\ &\text{subject to } \ && a_i^Tx \le b_i^T, i = 1, \cdots , 6 \\ \end{align*}\]

다음 그림에서 점선은 logarithmic barrier function \(\phi\)를 나타낸다.

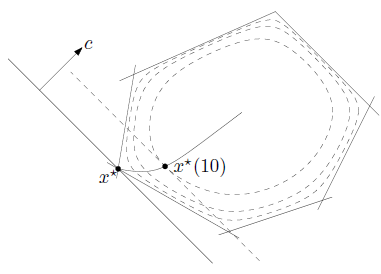
Central path가 \(t \to \infty\)일때 optimal \(x^*\)로 수렴하는 것을 볼 수 있다. 이때, hyperplane \(c^Tx = c^Tx(t)\)는 \(c^Tx(t)\)를 지나는 \(\phi\)의 level curve의 접선이다.