15-01-02 Log barrier function & barrier method

Barrier method를 소개하기 전에 먼저 indicator function을 barrier function으로 어떻게 근사할 수 있는지 살펴보도록 하자.

Approximation of indicator function

다음 그림을 보면 indicator function과 barrier function을 확인할 수 있다. 점선은 indicator function인 \(I_C\)이며 실선은 \(t = 0.5, 1, 2\)에 대한 barrier function \(\phi(x) = -1/t\log(-x)\)이다. Barrier function은 indicator function을 smooth하게 근사하고 있으며 \(t=2\)일 때 가장 좋은 근사를 보여주고 있다.

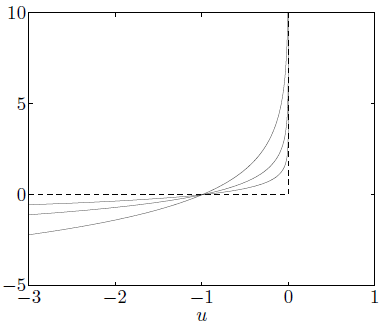
Logarithmic barrier function

\(h_1, \cdots , h_m : \mathbb{R}^n \to \mathbb{R}\)가 convex이고 두번 미분가능하다고 하자. set \(\{x : h_i(x) \lt 0, i = 1, \cdots , m \}\)에 대해 다음 함수를 logarithmic barrier function이라고 한다.

\begin{align} \phi(x) = - \sum_{i=1}^{m} \log(-h_i(x)) \end{align}

여기서 set은 interior of feasible set \(C\)로 non-empty라고 가정한다.

Barrier method

Barrier function을 사용해서 원래 문제를 다음과 같이 근사할 수 있다. 단, \(t\gt 0\)이다.

\[\begin{align} &\min_{x} && f(x) + \frac{1}{t} \phi(x) & \qquad & \min_{x} && tf(x) + \phi(x) \\ &\text{subject to } && Ax = b & \iff \qquad & \text{subject to } && Ax = b \\ \end{align}\]

이와 같이 정의된 문제를 newton’s method로 푸는 방법을 barrier method라고 한다.