14-04 Backtracking line search

지금까지 우리는 pure Newton’s method에 대해 살펴보았다. 하지만. 이 방법은 수렴이 보장되지 않으므로 backtracking line search를 활용하여 수렴을 보장하는 damped Newton’s method에 대해 살펴본다.

Damped Newton’s method

기존의 pure Newton’s method는 다음과 같은 update식을 반복하였다. (여기서 \(t=1\)이다.)

\begin{align} x^{+} = x -t(\nabla^{2}f(x))^{-1}\nabla f(x). \end{align}

Damped Newton’s method는 이전의 backtracking line search와 동일하게, update 과정에서 발산할 가능성이 있는 경우, 즉 update된 위치에서의 원함수 \(f\)의 값이 근사 함수의 값보다 크게되면 발산할 가능성이 존재하므로, step size \(t\)를 줄이는 과정을 거친다.

따라서 다음과 같은 과정을 추가하여 \(t\)의 update 여부를 결정한다.

\[\begin{align} &\text{with parameters }0<\alpha \leq \frac{1}{2}, 0<\beta<1, \\ &\text{while } f(x+tv)>f(x)+\alpha t \nabla f(x)^{T}v\\ &\text{shrink }t=\beta t \end{align}\]

여기서 \(v=-(\nabla^{2}f(x))^{-1}\nabla f(x)\)이고, \(\nabla f(x)^{T}v = -\lambda^{2}(x)\) 이다.

Example : logistic regression

예제로, n = 500, p = 100인 logistic regression에 대해 각각 backtracking을 적용한 gradient descent와 newton’s method의 iteration에 따른 수렴속도를 비교해본다.

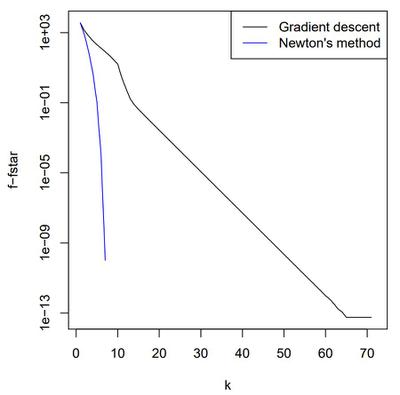
Newton’s method는 gradient descent보다 훨씬 더 빠른 수렴속도를 보인다. 다음 장에서 부터는 이 수렴속도에 대하여 살펴본다.