14-02-03 Local convergence analyisis
Newton’s method의 두 번째 중요한 성질로는 특정 조건들을 만족하면, 해의 근처에서 수렴성이 보장된다는 것이다. 이를 local convergence라고 명명한다. 14-01에서부터 우리가 논해온 pure Newton’s method의 경우 수렴성이 보장되지 않기 때문에, 후에 이전에 6장에서 다루었던 backtracking line search를 동일하게 적용하여 step size를 조절하여 수렴성을 보장하는 damped Newton’s method를 고안하고, 이에 대한 수렴성을 분석한다.
정리 : \(F : \mathbb{R}^{n}\, \rightarrow \, \mathbb{R}^{n}\) 가 연속으로 미분가능(continuosly differentiable)하고, \(x^{\star} \in \mathbb{R}^{n}\) 가 함수 \(F\)의 근이라고 하자, 즉, \(F(x^{\star})=0\)이다. 이때 \(F^{'}(x^{\star})\)이 non-singular 하다면 아래의 (a), (b)를 만족한다.
(a) 만약 \(\| x^{(0)}-x^{\star} \|<\delta\)를 만족하는 양수의 \(\delta\)(>0)가 존재하고, Newton’s method가 정의되어 있으면 밑의 식(converges superlinearly)을 만족한다. \begin{align} \lim_{ k \rightarrow \infty } \frac{ || x^{ (k+1) }-x^{ \star } || } { || x^{ (k) }-x^{ \star } || } =0. \end{align}
(b) 만약 \(F^{'}\)가 \(x^{\star}\)의 근처에서 Lipshitz continuous하면, 밑의 식(quadratic convergence)을 만족하는 양수 K(>0)가 존재한다. \begin{align} ||x^{ (k+1) } - x^{ \star }|| \leq K || x^{ (k) }-x^{ \star }||^{2}. \end{align}
Proof of (a)
Taylor expansion으로 \(F(x^{\star})\)를 1st order까지 정리한다. 2nd order 이상의 항은 1st order의 norm의 상수배에 bound 되므로, little-o notation을 사용하여 다음과 같이 나타낼 수 있다. \begin{align} 0=F(x^{\star}) = F(x^{k}) +\nabla F(x^{k})(x^{\star}-x^{k})+o(||x^{k}-x^{\star}||).
\end{align} 양변에 \(\nabla F(x^{k})^{-1}\)를 곱하고 정리한다. little-o의 경우 상수항 취급되므로 이를 무시할 수 있다. \begin{align} x^{k}-x^{\star}-\nabla F(x^{k})^{-1} F(x^{k}) = o(||x^{k}-x^{\star}||). \end{align} Newton’s method \(x^{k+1}=x^{k}-\nabla F(x^{k})^{-1}F(x^{k})\)를 이용하여 아래와 같은 결과를 얻을 수 있다. \begin{align} x^{k+1}-x^{\star}=o(||x^{k}-x^{\star}||), \end{align} 따라서, \(x^{k} \neq x^{\star}\) 일 때, little-o의 limit-definition[wikipedia]를 이용하여 (a)를 보일 수 있다.
\begin{align} \lim_{k\rightarrow \infty} \frac{||x^{k+1}-x^{\star}||}{||x^{k}-x^{\star}||} = \lim_{k\rightarrow \infty}\frac{o(||x^{k}-x^{\star}||)}{||x^{k}-x^{\star}||}. \end{align}
Proof of (b)
과정이 [14-05]의 Damped phase에서의 수렴 속도가 quadratic함을 증명하는 과정과 동일하다. 따라서 생략한다.
Example : divergence case
pure Netwon’s method로 수렴이 보장되지 않는 예시를 간략하게 살펴본다.
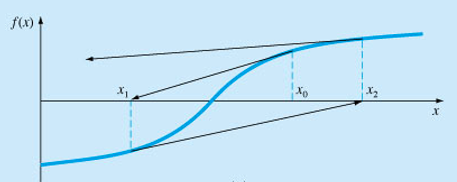
그림에서와 같이 initial point \(x_0\)에 따라서, 해가 발산할 수 있음이 확인된다.