14-01-01 Newton's method interpretation
이 페이지에서는 앞서 다루었던 update step이 원 함수 \(f\)의 quadratic approximation으로부터 어떻게 유도되는지 살펴본다. 또한 6장에서 다룬 gradient descent의 update step와 비교해본다.
Newton’s method update step
함수 \(f\)의 2차 테일러 근사(quadratic approximation)은 다음과 같다.
\[\begin{align} f(y) \approx f(x) + \nabla f(x)^{T}(y-x) +\frac{1}{2}(y-x)^{T}\nabla^{2}f(x)(y-x),\\\\ f_{approx}(y) = f(x) + \nabla f(x)^{T}(y-x) +\frac{1}{2}(y-x)^{T}\nabla^{2}f(x)(y-x). \end{align}\]
여기서 \(y\)는 다음 스텝의 \(x\) 값인 \(x^{+}\)이다. 또한 quadratic approximation을 \(f_{approx}\)로 정한다.
우리는 이 \(f_{approx}\) 즉, quadratic approximation을 최소로 만드는 입력 \(y\)를 찾으려 한다. 이때 \(f_{approx}\)는 convex이므로 위 식의 gradient를 0로 만드는 입력 \(y\)가 \(f_{approx}\)를 최소로 만들 것이다. 이 결과가 Newton’s method에서의 step update 식이 된다. 아래 식의 미분은 y에 대한 미분 임을 기억하자.
\[\begin{align} \nabla f_{approx}(y) &= \nabla f(x) +\frac{1}{2} \Big((\nabla^{2} f(x))^{T}(y-x)+(y-x)^{T}\nabla^{2}f(x)\Big)\\\\ &=\nabla f(x) +\nabla^{2} f(x)(y-x)\\\\ & = 0,\\\\ \Leftrightarrow y &= x-(\nabla^{2}f(x))^{-1}\nabla f(x). \end{align}\]
Gradient descent update step
gradient descent에서는 함수 \(f\)의 2차 테일러 근사 항을 사용하고, 2차 항의 경우 실제 2차 미분 결과가 아닌, 정방행렬(identity matrix)과 이를 \(t\)로 나눈 값으로 가정한다.
\[\begin{align} f(y) \approx f(x) + \nabla f(x)^{T}(y-x) +\frac{1}{2t}\|{y-x}\|_{2}^{2},\\\\ f_{approx}(y) = f(x) + \nabla f(x)^{T}(y-x) +\frac{1}{2t}\|{y-x}\|_{2}^{2}.\\\\ \end{align}\]
Newton’s method와 동일하게 위 근사식의 gradient가 0인 \(y\)값, 즉 \(x^{+}\)를 정할 수 있다.
\[\begin{align} \nabla f(y) &= \nabla f(x) + \frac{1}{t}(y-x), \\\\ &= 0,\\\\ y &= x-t\nabla f(x). \end{align}\]
이 결과는 gradient descent의 step update와 동일하다.
gradient descent의 자세한 내용은 gradient descent 장에서 참고할 수 있다.
Example
예시로써, 함수 \(f = (10x_{1}^{2}+x_{2}^{2})/2+5log(1+e^{-x_{1}-x_{2}})\)에 대하여 거의 동등한 길이의 step을 진행한다고 가정하고, 즉 newton’s method의 업데이트 크기만큼 매번 gradient descent에서의 step size를 정하고, gradient descent(검정)와 Newton’s method(파랑)의 step에 따른 수렴 방향을 비교해본다.
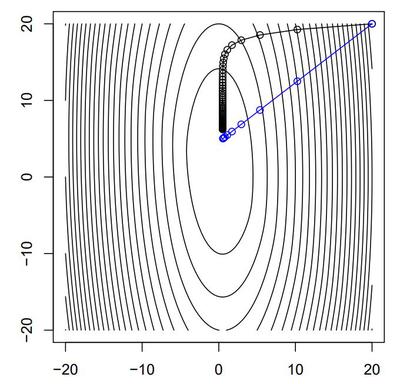
Fig 1에서도 알 수 있다시피, gradient descent는 2차 미분 항을 정방행렬에 상수가 곱해진 값으로 가정하고 gradient를 계산하기 때문에, 등고선(contour)의 접선 방향에 수직하게(perpendicular) 수렴함을 확인할 수 있고, Newton’s method에 비해 느린 수렴 속도를 보인다. 이 후의 나머지 장에서는 Newton’s method의 성질과 특징, 수렴성, 예시 등을 다룬다.