13-05 Dual cones

Dual cones

Cone \(K ⊆ \mathbb{R}^n\) 가 존재 한다. (앞서 02-06-01에서 다루었던 내용을 다시 되짚어 보면 그 뜻은 \(x \in K, t ≥ 0 \to tx \in K\)와 같다.)

\[K∗ = \{ y : y^Tx ≥ 0 \text{ for all } x \in K \}\]

이를 일컬어 dual cone 이라 하며, 이는 항상 convex cone이다. (심지어 \(K\) 가 convex가 아니어도 성립한다.)

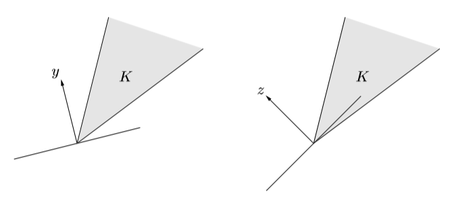
[주의]

\(y \in K∗ \iff \text{ the halfspace } \{ x : y^Tx ≥ 0 \} \text { contains } K\) (From B & V page 52)

여기서 중요한 성질은 \(K\)가 closed이고 convex cone이면 \(K^{∗∗} = K\)이다.

Examples:

• Linear subspace의 dual cone \(V\)는 \(V^{⊥}\)이다. 즉, orthogonal complement이다. E.g., \((row(A))^{∗} = null(A)\)

• Norm cone의 dual cone \(K = \{ (x,t) \in \mathbb{R}^n+1 : \| x \|≤ t \}\)은 그 dual norm \(K^{∗} = \{ (y,s) \in \mathbb{R}^{n+1} : \| y \|_{∗} ≤ s \}\)의 norm cone 이다.

• Positive semidefinite cone \(\mathbb{S}^n_+\)은 self-dual의 convex cone 이다. 즉\((\mathbb{S}^n_+)^{∗} = \mathbb{S}^n_+\)라는 뜻이다.

과연 왜 그럴까? 확인해보자

\[Y \succeq 0 \iff tr(Y X) ≥ 0 \text{ for all } X \succeq 0\]

\(X\)의 eigenvalue decomposition

Dual cones and dual problems

Consider the cone constrained problem 제약 조건이 있는 cone을 살펴보자.

\[\min_x f(x) \text{ subject to } Ax \in K\]

\(I^{∗}_K(y) = \max_{z\in K} z^Ty\)가 \(K\)의 support function 일때 위 수식의 dual problem은 다음과 같다.

\[\max_u −f^∗(A^Tu)−I^∗_K(−u)\]

여기서 \(K\)가 cone일 경우 다음 처럼 쉽게 정의 할 수 있다.

\[\max_u −f^∗(A^Tu) \text{ subject to } u \in K^{∗}\]

여기서 \(K^{∗}\)는 \(K\)의 dual cone 이다. because \(= I_K^{*}(-u) \ I_{K^{*}}(−u)\)

많은 다른 유형의 제약 조건이 cone의 제약 조건으로 나타날 수 있기 때문에 이것은 꽤 유용하다.