13-04 Conjugate function

주어진 함수 \(f : \mathbb{R}^n → \mathbb{R}\), 에 대하여 conjugate \(f^{∗} : \mathbb{R}^n → \mathbb{R}\)는 다음과 같이 정의 한다.

\[f^{∗}(y) = \max_x y^Tx−f(x)\]

[Note]

\(f^{∗}\)는 convex(affine) 함수 \(y^Tx - f(x)\)의 pointwise maximum이므로 항상 convex이다. (여기서 \(f\)는 반드시 convex일 필요는 없다.)

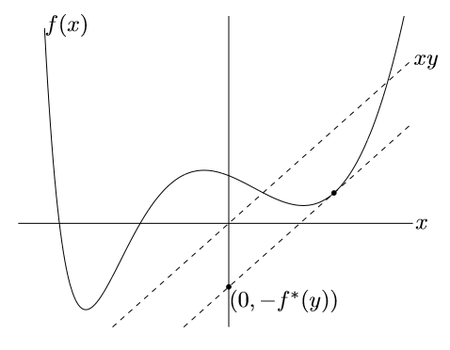
\(f^{∗}(y)\)는 선형 함수 \(y^Tx\)와 \(f(x)\) 간의 maximum gap이다. (From B & V page 91)

미분 가능한 \(f\)에 대한 conjugation을 Legendre 변환이라고 부른다.

Properties:

• Fenchel’s inequality: for any \(x,y, f(x) + f^{∗}(y) ≥ x^Ty\)

\(f(x) + f^{∗}(y) ≥ x^Ty \iff f^{*}(y) \ge x^Ty - f(x)\) \(f^{*}(y) = \max_z z^Ty - f(x)\)

• conjugate의 conjugate은 \(f^{∗∗}\)이므로 \(f^{∗∗} ≤ f\) 가 성립한다.
• 여기서 만약\(f\)가 closed이고 convex 이면, \(f^{∗∗} = f\)과 같다.
•\(f\)가 closed이고 convex 이면, 모든 \(x,y\)에 대해 다음이 성립한다.

\[\begin{align} x ∈ ∂f^{∗}(y) &\iff y ∈ ∂f(x) \\\ &\iff f(x) + f^{∗}(y) = x^Ty \\\ \end{align}\]

• \(f(u,v) = f_1(u) + f_2(v)\)이면, \(f^{∗}(w,z) = f_1^{∗}(w) + f_2^{∗}(z)\)이 성립한다.

Examples:

• \(f(x)\)가 아래와 같은 Simple quadratic일 경우를 살펴보자

\(f(x) = \frac{1}{2}x^TQx\), where \(Q \succ 0\)

그러면 \(y^Tx− \frac{1}{2}x^TQx\)는 \(y\)에 strictly concave이고, \(x = Q^{−1}y\) 에서 최대가 된다. 즉 \(f^{∗}(y) = \frac{1}{2}y^TQ^{−1}y\)

[Proof]

\[\begin{align} f^{*}(y) & = \max_x \left( y^Tx -\frac{1}{2}x^TQx \right) \\\ & = -\min_x \left(\frac{1}{2}x^TQx- y^Tx \right), x^{\star} = Q^{-1}y \\\ & = -\frac{1}{2}y^TQ^{-1}QQ^{-1}y + y^TQ^{-1}y \\\ & = \frac{1}{2}y^TQ^{-1}y \\\ \end{align}\]

Fenchel’s inequality: for any \(x, y\) \(\frac{1}{2} x^TQx + \frac{1}{2} y^TQ^{-1}y \ge x^Ty\)

• Indicator function: \(f(x) = I_C(x)\)이면, 그 conjugate 은 다음과 같다.

\(f^{∗}(y) = I^{∗}_C(y) = \max_{x ∈ C} y^Tx\) called the support function of \(C\)

• Norm: \(f(x) = x \rVert\)이면, 그 conjugate은 다음과 같다.

\(f^{∗}(y) = I_{\\{ z : \rVert z \rVert_{∗} ≤ 1 \\}}(y)\) where \(\rVert · \rVert_{∗}\) is the dual norm of \(\rVert · \rVert\)