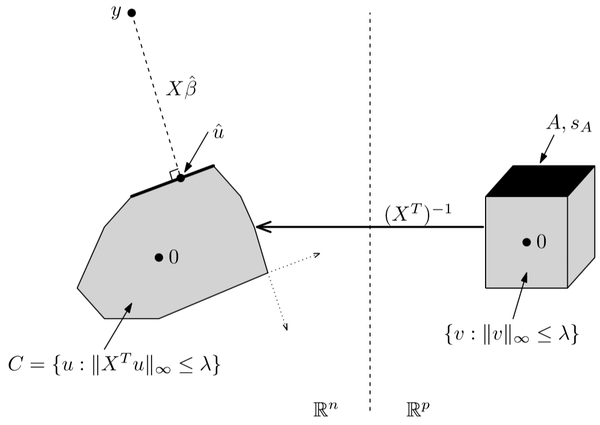
13-04-01 Example lasso dual

\(y ∈ \mathbb{R}^n, X ∈ \mathbb{R}^{n×p}\)인 lasso 문제를 다시 살펴보자

\[\min_β \frac{1}{2} \rVert y−Xβ \rVert^2_2 + λ\rVert β \rVert_1\] \[f(β) = \frac{1}{2} \rVert y - Xβ \rVert^2_2 + λ\rVert β \rVert_1\] \[L(β) = f(β)\\\] \[\min_β L(β) = f^{\star}\\\]

위 수식의 dual 함수는 constant 이다. (= \(f^{*}\)). 그러므로 primal 문제를 다음과 같이 변형할 수 있다.

\[\min_{β,z} \frac{1}{2} \rVert y−z \rVert^2_2 + λ \rVert β \rVert_1 \text{ subject to } z = Xβ\]

변형된 dual 함수는 아래와 같다.

\[\begin{align} g(u) &= \min_{β,z} \frac{1}{2} \rVert y−z \rVert^2_2 + λ \rVert β \rVert_1 + u^T(z−Xβ) \\\ &= \frac{1}{2} \rVert y\rVert^2_2 - \frac{1}{2} \rVert y−u \rVert^2_2 − I_{\{ v : \rVert v \rVert_∞ ≤ 1 \}}(X^Tu/λ) \\\ \end{align}\]

[Proof]

\[\begin{align} g(u) &= \min_{β,z} \frac{1}{2} \rVert y−z \rVert^2_2 + λ \rVert β \rVert_1 + u^T(z−Xβ) \\\ &= \underbrace{ \left( \min_z \frac{1}{2} \rVert y - z \rVert^2_2 + u^Tz \right)}_{①} + \underbrace{\left( \min_β λ \rVert β \rVert_1 + u^TXβ \right)}_{②} \\\ \end{align}\] \[z^{\star} = y - u\]

\(\begin{align} \text{①} \cdots \left( \min_z \frac{1}{2} \rVert y - z \rVert^2_2 + u^Tz \right) &= \frac{1}{2} \rVert u \rVert^2_2 + u^T(y - u) \\\ &= -\frac{1}{2} \rVert y - u \rVert^2_2 + \frac{1}{2} \rVert y \rVert^2_2 \\\ \end{align}\) \(\begin{align} \text{②} \cdots \left( \min_β λ \rVert β \rVert_1 + u^TXβ \right) &= - λ \max_β \frac{u^Tx}{λ} β - \rVert β \rVert_2 \\\ &= - λ \left( \lVert \frac{u^Tx}{λ} \rVert_∞ ≤ 1 \right) \\\ &= - λ \left( \lVert u^Tx \rVert_∞ ≤ λ \right) \\\ \end{align}\) \(\begin{align} \therefore g(u) &= -\frac{1}{2} \rVert y - u \rVert^2_2 + \frac{1}{2} \rVert y \rVert^2_2 + - λ \left( \lVert u^Tx \rVert_∞ ≤ λ \right) \\\ &= \frac{1}{2} \rVert y \rVert^2_2 - \frac{1}{2} \rVert y−u \rVert^2_2 − I_{\{ v : \rVert v \rVert_∞ ≤ 1 \}}(X^Tu/λ) \\\ \end{align}\)

따라서, lasso dual 문제는 아래와 같다.

\[\max_u \frac{1}{2} \left( \rVert y \rVert^2_2 − \rVert y−u \rVert^2_2 \right) \text{ subject to } \rVert X^Tu \rVert_∞ ≤ λ\]

다음은 위식과 동치이다.

\[\min_u \rVert y−u \rVert^2_2 \text{ subject to } \rVert X^Tu \rVert_∞ ≤ λ\]

[Check]

Slater’s condition을 을 충족하여 strong duality를 만족한다.

\[\text{strong duality } \implies (β^{\star}, z^{\star})\] \[\text{ must minimize } L( β, z, u^{\star} ) \text{ over } -u, β, z\]

[note]

지난 문제에서의 최적값(optimal value)은 optimal lasso objective 값이 아니었다. 게다가, 주어진 dual solution \(u\)와 lasso solution \(β\)는 \(Xβ = y−u\)를 만족한다.

이는 KKT stationarity condition을 통해 만족한다. \(z (즉, z−y + β = 0)\).

따라서 lasso는 dual residual을 만족한다.