12-03 Example water-filling
다음과 같은 컨벡스 최적화 문제가 주어졌다고 하자.
\[\begin{align} &\min_{x} &&{- \sum_{i=1}^n \log(\alpha_i + x_i)} \\\\ &\text{subject to} &&{x \succeq 0, 1^Tx = 1},\\\\ &\text{where } \alpha_i > 0. \end{align}\]
이 문제는 n개의 communication channels에 전력을 할당하는 문제이며, 정보이론(information theory)에서 대두되었다. 변수 \(x_i\)는 i번째 채널에 할당되는 송신기의 출력을 나타내며, \(\log(\alpha_i + x_i)\)는 해당 채널의 capacity 또는 communication rate를 나타낸다. 즉, 이 문제는 communication rate의 총합을 최대화하기 위해 각 채널에 얼마만큼의 전력을 할당해야 하는지 결정하기 위한 문제이다 [1].
Inequality constraint \(x^\star \succeq 0\)와 equality constraint \(1^Tx^\star = 1\)에 대한 Lagrange multipliers를 각각 \(\lambda^\star \in \mathbb{R}^n\), \(\nu^\star \in \mathbb{R}\)라고 하자. 이때 주어진 문제에 대한 KKT conditions는 다음과 같다.
\[\begin{align} x^\star \succeq 0, \\\\ 1^Tx^\star = 1, \\\\ \lambda^\star \succeq 0, \\\\ \lambda_i^\star x_i^\star = 0, \text{ } i = 1, \dots, n, \\\\ -1 / (\alpha_i + x_i^\star) - \lambda_i^\star + \nu^\star = 0, \text{ } i= 1, \dots, n. \end{align}\]
KKT conditions를 통해 얻은 수식들을 이용하면 \(x^\star, \lambda^\star, \nu^\star\)를 해석적으로(analytically) 구할 수 있다. 일단 \(\lambda^\star\)를 slack variable로 사용하여 위 수식에서 \(\lambda^\star\)를 제거한다.
\[\begin{align} x^\star \succeq 0, \\\\ 1^Tx^\star = 1, \\\\ x_i^\star(\nu^\star - 1 / (\alpha_i + x_i^\star)) = 0, \text{ } i = 1, \dots, n, \\\\ \nu^\star \ge 1/(\alpha_i + x_i^\star), \text{ } i= 1, \dots, n. \end{align}\]
이는 stationarity와 complementary slackness에 의해 다음과 같이 정리된다.
\[x_i^\star = \begin{cases} 1 / \nu^\star - \alpha_i &\nu^\star < 1/\alpha_i \ \\\\ 0 &\nu^\star \ge 1/\alpha_i\\\\ \end{cases} = \max\{0, 1/\nu^\star - \alpha_i \}, \quad i = 1, \dots, n.\]
또한 조건 \(1^T x^\star = 1\)에 의해 \(x_i^\star, i = 1, \dots, n\)은 합산하여 1이 된다.
\[\sum_{i=1}^n \max\{0, 1/\nu^\star - \alpha_i \} = 1.\]
위 등식의 좌항은 \(1/\nu^\star\)에 대한 piecewise-linear increasing function이므로 이 등식은 고정된 \(\alpha_i\)에 대해 unique solution을 갖는다.
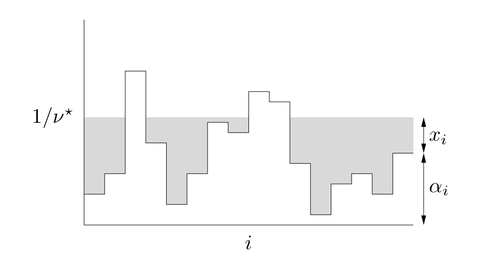
이 solution method를 일컬어 water-filling이라고 부른다. 이 문제는 \(\alpha_i\)가 patch \(i\)에 대한 ground level이라고 할 때, 아래 그림과 같이 물의 높이가 \(1/\nu^\star\)가 되도록 각 영역에 물을 붓는 것으로 생각할 수 있다. 우리는 전체 물의 양이 1이 될 때까지 물을 붓도록 한다.