10-05 Matrix Games

이번 장에서는 게임이론에서의 primal LP, dual LP의 예시인 mixed strategies for matrix games에 대해서 살펴본다. 설정은 두명의 player, J와 R, 그리고 payout matrix \(P\)가 있다고 하자.

Game Setup

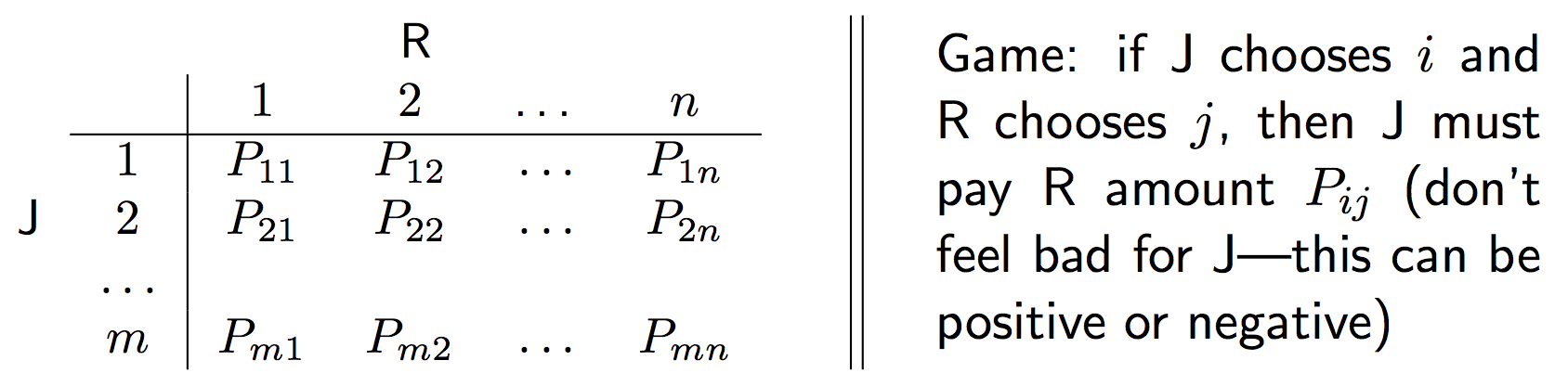
payout matrix는 만약 J가 전략 \(i\)를 선택하고(row), R이 전략 \(j\)를 선택했을때(column), J가 R에게 주어야 하는 보상의 크기이다(\(P_{ij}\)). 하지만 이 값이 양수라면, J가 R에게 해당 matrix의 크기만큼의 보상을 주고, 음수라면 R이 J에게 해당 matrix의 크기만큼의 보상을 주게 된다.

이러한 setting을 zero-sum setting이라고도 하는데, R이 받게 될 혹은 지불해야할 보상을 \(r_{R}\), J의 보상을 \(r_{J}\)라 할 때, 매 게임에서 보상의 결과는 \(r_{R} = - r_{J}\)이고, 두 보상의 총합은 항상 0이 된다.

또한 두 명의 player가 모두 mixed strategies를 사용한다고 가정한다, mixed strategies는 각자의 선택이 특정한 확률분포를 따른다는(혹은 특정한 확률분포에서 sampling 된다는) 가정이다.

\[\begin{align} x : P(\text{J chooses i}) = x_{i}, \qquad i=1,...m\\\\ y : P(\text{R chooses j}) = y_{j}, \qquad j=1,...n.\\\\ \end{align}\]

서로가 서로의 mixed strategy, 즉 확률분포를 알고 있다면, 각자는 각자가 얻을 것으로 기대하는 payout, 즉 expected payout을 계산할 수 있다.

\[\begin{align} \sum_{i=1}^{m}\sum_{j=1}^{n}x_{i}y_{j}P_{ij} = x^{T}Py.\\\\ \end{align}\]

payout matrix의 부호가 J가 R에게 주는 크기로 정의되어 있음을 생각할 때, J는 R에게 최대한 주지 않으려 하기 때문에, 이 expected payout을 최소화(minimize)하려 할 것이고, R은 J에게서 최대한 받고 싶어하기 떄문에, 이 expected payout을 최대화(maximize)하려 할 것이다.

이제 두 player의 입장에서 각자가 상대의 mixed strategy를 고려하여, 이 expected payout을 최대화(R의 입장) 혹은 최소화(J의 입장)하려는 관점을 살펴보고, 서로가 서로를 optimal하게 행동하는 전제하에, 두 입장에서 유도되는 optimal strategy를 구하고, 결과적으론 Von Neumman’s minimax theorem에 의해 두 결과가 같다는 것을 확인할 것이다.

Minimizing Expected Payout : J’s Perspective

먼저 R이 J의 strategy \(x\)를 알고 있다고 가정하자. R은 expected payout \(x^{T}Py\)를 maximize하고자 할 것이다.

\[\begin{align} \max\{x^{T}Py : y\geq0, 1^{T}y = 1\} = \max_{i=1,...n}(P^{T}x)_{i}.\\\\ \end{align}\]

이때 R은 식의 내용처럼 \((P^{T}x)_{i}\) 중 가장 큰 값을 갖는 i(row index)를 찾게되고, 이 i에 대응되는 \(y_{i}\)를 1로 가지고 나머지의 row index에 대해선 0을 가지는 strategy가 R에게 있어서 expected payout을 maximize하는 strategy일 것이다.

R이 위처럼 최적으로 행동할 것을 알고 있을 때, J의 최적의 strategy는 밑의 식을 만족하는 distribution \(x\)일 것이다.

\[\begin{align} & \min_{x} & &\max_{i=1,...n} (P^{T}x)_{i}\\\\ & \text{subject to} & & x\geq 0, 1^{T}x =1.\\\\ \end{align}\]

Convex function의 maximization 또한 convex function이 된다. 이를 첫 번째 관점의 문제 정의라고 칭할 것이다. 또한 이 최적화 문제의 해를 optimal expected payout \(f^{*}_{1}\)이라고 정하자. 또 하나 유념할 점은 게임참가자, 즉 player들이 모두 최적으로 행동한다는 가정이 기본적인 형태의 게임이론 formulation에서 가정이 된다.

Maximizing Expected Payout : R’s Perspective

두 번째 관점으로 J가 R의 strategy \(y\)를 알고 있다고 가정하자. J는 expected payout을 minimize하고자 할 것이다.

\[\begin{align} \min \{x^{T}Py : x\geq0, 1^{T}x = 1\} = \min_{j=1,...n}(Py)_{j}.\\\\ \end{align}\]

같은 논리로, J가 위처럼 최적으로 행동할 것을 알고 있을 때 R의 최적의 strategy는 밑의 식을 만족하는 distribution \(y\)이다.

\[\begin{align} & \max_{y} & & \min_{j=1,...m} (Py)_{j}\\\\ &\text{subject to} & &y\geq 0, 1^{T}y =1.\\\\ \end{align}\]

위와 마찬가지로 이를 두 번째 관점의 문제 정의라고 칭하고, 이 최적화 문제의 해를 \(f^{*}_{2}\) 라고 하자. player R이 이 expected payout을 maximize하고자 하기 때문에, 첫 번째, 즉, R이 J의 strategy를 미리 알고 있다는 가정 하에 결정되는 expected payout \(f^{*}_{1}\)이 두 번째 가정보다 더 크거나 같은 값을 가질 것이라 쉽게 예상할 수 있다. (\(f^{*}_{1}\geq f^{*}_{2}\))

Von Neumann’s minimax theorem

하지만, Von Neumann’s minimax theorem에 따르면 \(f^{*}_{1} = f^{*}_{2}\)가 된다. 실제 minimax theorem은 다음과 같다.

\[\begin{align} &\text{Let } X\subset \mathbb{R}^{N} \text{ and }Y\subset \mathbb{R}^{m} \text{ be compact convex sets. }\\\\ &\text{If } f:X\times Y\rightarrow \mathbb{R} \text{ is a continuous function that is convex-concave, i.e.}\\\\ &\qquad f(\cdot, y): X\rightarrow\mathbb{R} \text{ is convex for fixed }y, \text{ and}\\\\ &\qquad f(x, \cdot): Y\rightarrow\mathbb{R} \text{ is concave for fixed }x.\\\\ &\text{Then we have that} \\\\ &\min_{x\in X} \max_{y\in Y} f(x,y) = \max_{y\in Y} \min_{x\in X} f(x,y).\\\\ \end{align}\]

해당 내용의 증명은 생략한다.

Proof of each perspective having Primal and Dual relationship

이제 위 두 가지 관점의 경우에 대한 expected payout이 LP 문제로써 서로 primal, dual 관계이고, Von Neumman’s minimax theorem에 의하여 두 결과가 같다는 점을 이용하여, strong duality를 만족함을 보이고자 한다.

먼저 첫 번째 관점의 문제를 다음과 같이 reformulate 할 수 있다.

\[\begin{align} & \min_{x} \max_{i=1,...m} & &(P^{T}x)_{i}\\\\ &\text{subject to } & &x\geq 0, 1^{T}x = 1\\\\ \end{align}\] \[\begin{align} \Leftrightarrow{} \\\\ & \min_{x,t} & & t \\\\ &\text{subject to } & &x\geq0, 1^{T}x = 1, P^{T}x \preceq t. \\\\ \end{align}\]

\(t\)를 \(P^{T}x\)의 항들 중 가장 큰 값과 같게 만들어주는 문제로 reformulate 하였다.

이제 여기에 앞서 배운 duality의 두 번째 방법인 Lagrangian을 구하고, Lagrange dual function \(g\)를 구하면,

\[\begin{align} &L(x, t, u, v, y) &&= t-u^{T}x+v(1-1^{T}x)+y^{T}(P^{T}x-t1)\\\\ &g(u, v, y) &&= \min_{x,t} \quad L(x, t, u, v, y)\\\\ &&&= \begin{cases} v \qquad &\text{if } 1-1^{T}y = 0, Py-u-v1=0\\\\ -\infty \qquad &\text{otherwise.} \end{cases} \end{align}\]

\(u\)는 slack variable이므로, 이를 제거하고 식을 정리하면 다음과 같다.

\[\begin{align} &\max_{y,v} \qquad \quad && v\\\\ &\text{subject to }\quad && y\geq0, 1^{T}y = 1\\\\ &&& Py\geq v. \end{align}\]

이는 두 번째 관점의 문제의 primal LP이다. 따라서 두 관점은 dual 관계에 있고 두 문제의 optimal value는 같으므로, strong duality가 성립한다.

일반적으로 LP문제에서는, 향 후의 내용에서 다루지만, primal과 dual 중 하나만 feasible하다면 strong duality가 성립한다.