10-03 Max flow and min cut

Linear program의 duality에 대한 예시로 max flow min cut 문제에 대해 살펴보고자 한다.

Directed Graph, Condition of flow

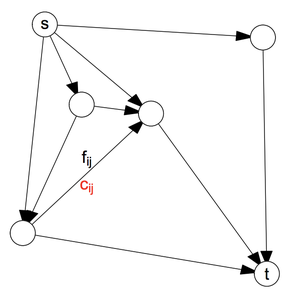
위와 같이 방향이 있는(directed) graph \(G = (V, E)\)가 있고, vertex i와 vertex j를 잇는 edge, \((i,j)\in E\), 즉 i에서 j로 흐르는 flow(유량)를 \(f_{ij}\)라고 하자. 각 edge에는 capacity, 즉 흐를 수 있는 최대 flow가 정해져있다. 이를 \(c_{ij}\)라 하자.

쉬운 예시로, source(s)에서 나오는 어떤 flow가 sink(t)로 흘러나가는 과정을 그래프로 나타낸 것이라 이해할 수 있다. 도시 배수/송전 계획, 물자 수송 등 다양한 문제에 적용될 수 있는 그래프 형태이다.

여기서 flow는 3가지 조건을 만족한다.

1. \(f_{ij}\)는 항상 0과 같거나 큰 양수이다 : \(f_{ij} \geq 0,\, (i,j)\in E\)
2. \(f_{ij}\)는 edge에 정해져 있는 최대 flow, 즉 capacity(한계 용량) \(c_{ij}\)보다 작아야 한다 : \(f_{ij}<c_{ij}, \, (i,j)\in E\)
3. source(flow가 나오는 지점, s) 또는 sink(flow가 나가는 지점, t)을 제외한 vertex k에 대해서, k로 들어가는 flow의 총량과 k에서 나오는 flow의 총량은 같다 : \(\sum_{(i,k)\in E}f_{ik} = \sum_{(k,j)\in E}f_{kj}, \, k\in V\backslash{s,t}\)

Relationship between Max flow and Min cut problem(1)

위처럼 정의된 graph와 flow에 대하여 대표적으로 알려진 두 가지 문제, max flow 문제, min cut 문제와 이 둘의 관계에 대해 살펴볼 것이다.

결론부터 말하자면, max flow 문제는 LP 문제이고, min cut 문제는 integer program인데, max flow 문제의 dual은 min cut 문제를 LP relaxation한 것과 동일한 문제형태를 갖는다.

\[\begin{align} \text{Value of max flow} &\leq \text{dual LP of max flow}\\\\ &= \text{Optimal value for LP relaxed min cut}\\\\ &\leq \text{Capacity of min cut}\\\\ \end{align}\]

이 페이지에서는 dual과 relaxation의 역과정(LP 문제에 제약 조건을 추가하여, integer program으로 변환)으로 다음과 같은 부등호 관계를 보일 것이다, 여기선 다루지 않지만, 실제론 이 세 결과가 모두 같다.

이를 max flow min cut theorem이라 부르며, 네트워크의 최대 flow는 cut의 최소 capacity와 같다는 정리이다.

좀 더 일반화하여 보면, 특정 조건에서 primal 문제와 dual 문제의 optimal value가 동일한 값을 가지는 경우가 있는데 이때를 strong duality 관계에 있다고 한다.

LP 문제에서는 두 primal, dual 문제 모두가 infeasible한 경우를 제외하고는 strong duality를 가진다. 이에 대한 내용은 11장에서 다루게 된다.

먼저 두 가지 문제에 대하여 살펴보고, max flow 문제에서 dual을 유도하고, 이 dual 문제에서 문제에 특정 조건을 추가함으로써(relaxation의 역과정) min cut 문제로 변환 됨을 보인다.

Max flow problem

Max flow problem이란 위 조건을 만족하는 그래프에 대해서 s에서 t로 흘러가는 flow의 최댓값을 찾는 문제이다.

\[\begin{align} &\max_{f\in {\mathbb{R}^{|E|}}} &&{\sum_{(s,j)\in E} f_{sj}}\\\\ &\text{subject to} &&{f_{ij}\geq 0,\,f_{ij}\leq c_{i,j}\,\, \text{for all }(i, j)\in E}\\\\ &&&{\sum_{(i, k)\in E}f_{ik}=\sum_{(k,j)\in E}f_{kj}}\,\, \text{for all }k\in V \backslash \{s,t\}.\\\\ \end{align}\]

Min cut problem

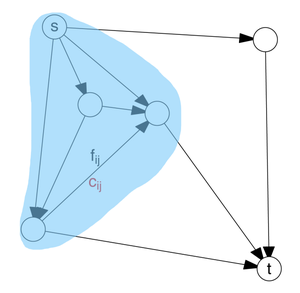
Min cut 문제는 graph의 전체 vertex를 그림에서처럼 색칠된 영역, 색칠되지 않은 영역 두 집합에 나눠서 속하게 하는데, 한 집합에는 source를 포함하고, 나머지 집합에는 sink를 포함하되, 나머지 vertex는 임의로 두 집합 중 하나에 속하게 나눈다(여기서는 source를 포함하는 집합을 A, sink를 포함하는 집합을 B라고 할 것이다),이때 집합 A에서 B로 진행하는 방향의 edge들의 capacity 총합을 cut이라고 정의한다.

다시 말해, cut은 source와 sink를 각각 다른 partition에 존재하게 구분하는 graph의 vertex partition이다. min cut은 graph가 주어졌을 때 이 cut의 최솟값을 찾는 문제이다. 일반적으로 정의되는 min cut 문제의 경우 directed graph 상에서 정의되기 때문에, 항상 source \(x_{s}=1\), sink \(x_{t}=0\)을 만족한다. 아래의 문제 정의에는 이 부분이 생략되어 있다.

\[\begin{align} &\min_{b\in {\mathbb{R}^{|E|}},\, x \in {\mathbb{R}^{|V|}} } &&{\sum_{(i,j)\in E} b_{ij}c_{ij}}\\\\ &\text{subject to} &&{b_{ij} \geq x_{i}-x_{j}}\\\\ &&&{b_{ij},\,x_{i},\,x_{j}\,\in \{ 0,1 \} }\\\\ &&&\text{for all }i, j.\\\\ \end{align}\]

직관적으로 생각하면, max flow 문제는 source에서 나오는 flow의 최댓값을 찾는 문제이고, min cut 문제는 source 집합에서 sink 집합으로 보낼 수 있는 전체 capacity의 최솟값을 찾는 문제이므로, 어렴풋이나마 이 둘의 문제가 비슷함을 알 수 있다.

Dual of Max flow problem

Max flow의 최적화 문제에 대하여 dual을 구해보자.

먼저 constraint에 대하여 dual variable을 순서대로 \(a_{ij}, b_{ij}, x_{k}\)로 정의한다. max 문제의 dual의 경우 upper bound를 minimize하는 형태가 될 것이므로, 정리한 형태가 primal objective의 upper bound를 가지는 primal objective \(\leq\) sth의 형태가 되어야 한다. 따라서, constraint에 대하여 \(f_{ij}\)의 upper bound를 찾는 방향으로 식을 정리한다. 이를 정리하면 다음과 같다.

\[\begin{align} \sum_{(i,j)\in E} {\Big(-a_{ij}f_{ij}+b_{ij}(f_{ij}-c_{ij})\Big)} + \sum_{k \in V\backslash \{s,t\}} x_{k}\Big( \sum_{(i,k)\in E} f_{ik} - \sum_{(k,j)\in E } f_{kj} \Big)\leq 0\\\\ \text{for any }a_{ij}, b_{ij} \geq 0, (i, j)\in E, \text{ and } x_{k}, k\in V \backslash \{s,t\}. \end{align}\]

primal LP의 목적함수와 관계된 \(f\)항을 좌항으로, 그 나머지는 우항으로 정리한다.

그 다음, 이 과정에서 우리가 원하는 것은 primal LP의 상한(upper bound)이므로, 좌항의 \(f\) 앞에 곱해져 있는 항들의 결과가 primal LP의 목적함수와 일치하도록 만드는 식을 찾는다.

이 식을 만족하도록 하는 조건이 dual LP에서의 constraint가 된다.

즉, \(f_{ij}\)의 식이 \(\sum_{(s,j)\in E}f_{sj}\)에서만 1을 갖고 나머지가 0이 되도록 정리한다.

이 과정을 조금 더 자세히 보면 다음과 같다.

\[\begin{align} \sum_{(i,j)\in E}{\Big((b_{ij}-a_{ij})f_{ij}\Big)}+\sum_{k\in V\backslash \{s,t\}}{x_{k}\Big(\sum_{(i,k)\in E}{f_{ik}}-\sum_{(k,j)\in E}{f_{kj}}\Big)} \leq \sum_{(i,j)\in E}b_{ij}c_{ij}. \end{align}\]

여기서, 우리는 \(i=s\)인 경우에 좌항의 결과가 \(\sum_{(s,j)\in E}f_{sj}\)이 되고, 다른 경우에 대해서는 0이 되게 식을 정리하는 것이 목표이다.

두 번째 시그마의 x항의 k는 source와 sink에 대해서는 포함되지 않음을 유의하면서, \(i=s, j\neq t\)인 경우, \(i\neq s, j=t\)인 경우, \(i\neq s,j\neq t\)가 아닌 경우로 나누어 좌항을 정리할 수 있다.

Case 1. \(i = s, j \neq t.\)

\(x_{k}\)에 곱해진 항에 대해서 \(k=j\)인 경우를 제외하고는, flow의 세번째 조건에 의해 소거된다. 따라서, 두 번째 항의 \(x\)항에 대한 시그마를 다음과 같이 정리할 수 있다.

\[\begin{align} &=\sum_{(s,j)\in E}{\Big((b_{sj}-a_{sj})f_{sj}\Big)}+x_{j}\sum_{(s,j)\in E}{f_{sj}}+\sum_{k\in V\backslash \\{s,t,j\\}}{x_{k}\Big(\underbrace{\sum_{(s,k)\in E}{f_{sk}}-\sum_{(k,j)\in E}{f_{kj}}}_{=0}\Big)} \\\\ &=\sum_{(s,j)\in E}{\Big(b_{sj}-a_{sj}+x_{j}\Big)f_{sj}}, \ j \in V \backslash \{s,t\},\\\\ \end{align}\]

Case 2. \(i \neq s, j = t.\)

\(x_{k}\)에 곱해진 항에 대해서 \(k=i\)인 경우를 제외하고는, flow의 세 번째 조건에 의해 소거된다. 따라서, 두 번째 항의 \(x\)항에 대한 시그마를 다음과 같이 정리할 수 있다.

\[\begin{align} &=\sum_{(i,t)\in E}{\Big((b_{it}-a_{it})f_{it}\Big)}-x_{i}\sum_{(i,t)\in E}{f_{it}}+\sum_{k\in V\backslash \{s,t,i\}}{x_{k}\Big(\underbrace{\sum_{(i,k)\in E}{f_{ik}}-\sum_{(k,t)\in E}{f_{kt}}}_{=0}\Big)} \\\\ &=\sum_{(i,t)\in E}{\Big(b_{it}-a_{it}-x_{i}\Big)f_{it}}, \ i \in V\backslash \{s,t\},\\\\ \end{align}\]

Case 3. \(i \neq s, j \neq t.\)

\(x_{k}\)에 곱해진 항에 대해서 \(k=i, k=j\)인 경우를 제외하고는, flow의 세 번째 조건에 의해 소거된다. 따라서, 두 번째 항의 \(x\)항에 대한 시그마를 다음과 같이 정리할 수 있다.

\[\begin{align} &=\sum_{(i,j)\in E}{\Big((b_{ij}-a_{ij})f_{ij}\Big)}+x_{j}\sum_{(i,j)\in E}{f_{ij}}-x_{i}\sum_{(i,j)\in E}{f_{ij}}+\sum_{k\in V\backslash \{s,t,i,j\}}{x_{k}\Big(\underbrace{\sum_{(i,k)\in E}{f_{ik}}-\sum_{(k,j)\in E}{f_{kj}}}_{=0}\Big)} \\\\ &=\sum_{(i,j)\in E}{\Big(b_{ij}-a_{ij}+x_{j}-x_{i}\Big)f_{ij}}, \ i, j \in V \backslash \{s,t\}. \\\\ \end{align}\]

primal LP의 목적함수는 이 세 가지 케이스 중 첫 번째 케이스에 \(b_{sj}-a_{sj}+x_{j}\) 항이 1이 되는 경우와 일치한다. 또한 나머지 케이스에 대해서는 곱해진 항을 0으로 만들어 주어 primal LP와 해당 식을 일치시켜주어, 좌항이 objective function, 우항이 upper bound인 형태를 완성할 수 있다.

\[\begin{align} &b_{sj}-a_{sj}+x_{j} = 1\\\\ &b_{it}-a_{it}-x_{i} = 0\\\\ &b_{ij}-a_{ij}+x_{j}-x_{i} = 0\\\\ &\text{Result in,} \\\\ &\sum_{(s,j)\in E}{f_{sj}} \leq \sum_{(i,j)\in E}{b_{ij}c_{ij}}. \end{align}\]

따라서, dual 문제는 dual variable \(a, b, x\)에 대하여 위에서 구한 upper bound(dual LP의 목적 함수)의 최소값을 찾는 형태이고, 이 최소값이 가장 좋은 upper bound가 된다. 일종의 dummy variable인 \(a\)를 조건을 유지하며 소거한다. 추가로, directed graph에서의 flow 조건을 추가하여 source에서 sink로 flow가 흘러간다는 조건을 constraint에 명시하면, 식은 다음과 같다.

\[\begin{align} &\min_{b\in {\mathbb{R}^{|E|}},\, x\in{\mathbb{R}^{|V|}}} &&{\sum_{(i,j)\in E} b_{ij}c_{ij}} \\\\ &\text{subject to} &&{b_{ij}+x_{j}-x_{i}\geq 0 \,\, \text{for all } (i,j)\in E}\\\\ &&&{b\geq 0, x_{s}=1,x_{t}=0}.\\\\ \end{align}\]

Dual LP to Integer program

이제 이 dual LP가 min cut 문제의 LP relaxation과 동일해짐을 보이고자 한다. 따라서 위 문제에 조건을 추가함으로써 integer program으로 바꾸는 과정을 거칠 것이다. 위 dual LP 문제에 대해서, \(x\)는 vertex가 s, t일 때를 제외하고 정의되어 있지 않은 형태이다. 따라서 문제의 scope를 좁히고자, s, t를 제외한 나머지의 vertex가 s 또는 t의 그룹에 속한다는 조건을 추가하여 문제를 해결해보자. 다시 말하면, 모든 vertex가 0 또는 1의 그룹에 속한다고 가정하자. 이는 min cut의 vertex partition을 정하는 것과 동일하다.

\[\begin{align} x_{i} \in \{0,1 \} \ \ \text{ for all }i\in V. \end{align}\]

1에 속하는 그룹을 집합 A로 정의하고, 0에 속하는 그룹을 집합 B로 정의하자. 또한 source(s)는 A에, sink (t)는 B에 속한다고 정하자.

위와 같이 정하면, \(b_{ij}\)는 집합 A에서 집합 B로 향하는 edge에 대해서는 1, 나머지에 대해선 0을 가지는 일종의 on/off의 역할을 한다.

이를 정리하면 다음과 같다.

\(\begin{align} &\text{Let } A= \{ i:x_{i}=1 \} ,\, B= \{ i:x_{i}=0 \} \\\\ &\text{note that } s \in A, \,t \in B, \text{ and }b_{ij}\geq x_{i}-x_{j} \,\,\,\, \text{for }\,(i,j) \in E, \,\, b\geq 0,\\\\ \end{align}\) \(\begin{align} \text{Simply say, } \qquad \begin{cases} b_{ij}=1 \qquad \text{if } i\in A, j\in B\\\\ 0 \qquad\qquad \text{otherwise}.\end{cases} \end{align}\)

위의 결과는 min cut 문제의 formulation과 동일하다.

Relationship between Max flow and Min cut problem(2)

즉, max flow problem의 dual problem은, min cut 문제에서 \(x\)의 s, t를 제외한 vertex를 0, 1로 포함된다는 조건을 없앤(relaxation)한 결과이다. optimal value of max flow \(\leq\) dual LP(upper bound)이고, 이 relaxation은 optimization variable의 domain scope를 확장시키므로, optimal value LP relaxed min cut \(\leq\) capacity of min cut의 관계를 가진다. 이 세 가지 결과를 정리하면 아래의 결과를 얻을 수 있다.

\[\begin{align} \text{Value of max flow} &\leq \text{Dual LP of max flow}\\\\ &= \text{Optimal value for LP relaxed min cut}\\\\ &\leq \text{Capacity of min cut}\\\\ \end{align}\]

이 세 가지 결과가 모두 같음에 대해서는 max-flow min-cut theorem[11] 에서, max flow min cut 문제를 푸는 대표적인 알고리즘으로는 Ford-Fulkerson algorithm[12]을 참고할 수 있다.