09-05-01 Accelerated proximal gradient method

Accelerated proximal gradient method

Proximal gradient descent를 가속화(accerleration)하게 되면 최적의 수렴 속도인 \(O(1/\sqrt{\epsilon})\)를 달성할 수 있다. Nesterov는 다음과 같은 네 가지 방식을 제안했으며 이 중 세 가지가 가속화 방법이다.

• 1983 : Smooth function에 대한 원래 가속화 방법
• 1988 : Smooth function에 대한 다른 가속화 방법
• 2005 : 원래 가속화 방법과 함께 nonsmooth function을 smoothing하는 기법
• 2007 : Composite function에 대한 가속화 방법

이제 Nesterov(1983)의 composite function에 대한 방법을 확장한 Beck과 Teboulle(2008)의 방법을 살펴보자.

Accelerated proximal gradient method

이전과 동일하게 \(g\)가 convex이고 미분가능하며 \(h\)는 convex일 때 다음과 같이 문제가 정의된다고 하자.

\begin{align} \min_x g(x) + h(x) \end{align}

Accelerated proximal gradient method는 \(x\)에서 다음 위치로 갈 때 방향이 급격히 바뀌지 않도록 \(x\)가 진행하던 방향을 고려하는 방식이다. 즉, 진행 방향에 모멘텀(momentum)을 주어 지금까지 진행하던 방향으로 계속 진행하려는 관성을 갖게 만든다.

알고리즘의 초기값은 \(x^{(0)} = x^{(−1)} \in \mathbb{R}^n\)로 둔다. 그리고, 모멘텀을 고려한 위치 \(v\)를 계산한 후 proximal gradient를 실행한다.

\[\begin{align} v & = x^{(k−1)} + \frac{k−2}{k + 1} (x^{(k−1)} −x^{(k−2)}) \\ x^{(k)} & = \text{prox}_{t_k} (v − t_k \nabla g(v)), k = 1,2,3,... \\ \end{align}\]

• 첫번째 스텝 \(k = 1\)에서는 \(x^{(k−1)} −x^{(k−2)}\)가 0이기 때문에 proximal gradient update와 동일하다.
• 그 다음 단계에서는 \(v\)는 이전 진행 방향인 \(x^{(k−1)} −x^{(k−2)}\)로 모멘텀을 갖는다. 이때, \(k\)가 작을수록 모멘텀 가중치는 작으며 \(k\)가 클수록 모멘텀 가중치는 커져서 1로 수렴한다.
• \(h = 0\)인 경우 accelerated gradient method와 같다.

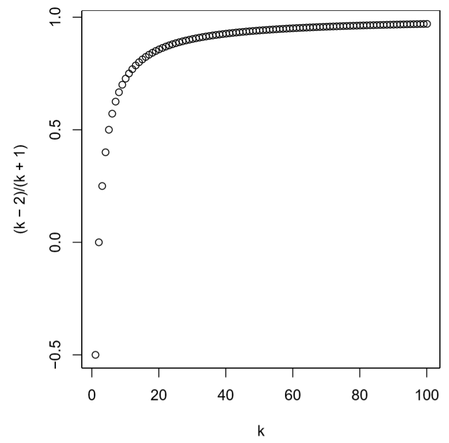
아래 그림에는 \(k\)의 변화에 따른 모멘텀 가중치의 변화를 보여주고 있다.

이 그림을 보면 k = 0일 때 값이 음수인데 이때 모멘텀 항이 0이 되기 때문에 문제가 되지는 않는다. k값이 증가할수록 가중치가 1에 가까워 지므로 값이 갱신될 때 좀 더 멀리 나아가면서 빠르게 수렴할 수 있도록 도와준다.

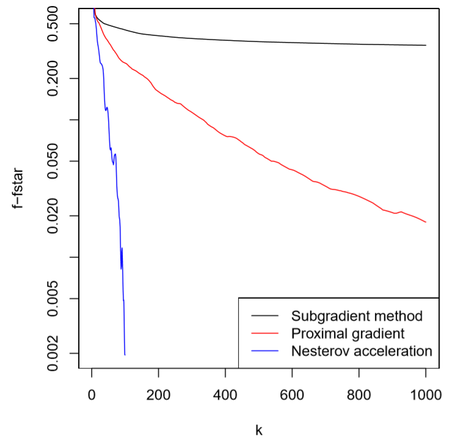
Lasso example

이전에 보았던 Losso 예시에 accelerated proximal gradient를 적용해 보면 다음 그림과 같은 결과를 얻을 수 있다. Accelerated proximal gradient subgradient나 proximal gradient에 비해 매우 빠른 성능을 갖고 있음을 알 수 있다.

그래프의 중간에 튀는 부분이 보이는데 이를 “Nesterov ripples”이라고 부른다. 따라서, accelerated proximal gradient는 monotonic decreasing하지 않기 때문에 descent 방법이 아니다.