09-04 Special cases

Special cases

Proximal gradient descent는 composite gradient descent 또는 generalized gradient descent라고도 한다.

그렇다면 왜 “generalized”라고 할까? 그 이유는 Proximal gradient descent가 다음과 같은 특별 케이스들을 모두 포함하기 때문이다.

• \(h = 0 \to\) gradient descent
• \(h = I_C \to\) projected gradient descent
• \(g = 0 \to\) proximal minimization algorithm

따라서 이 알고리즘들은 모두 \(O(1/\epsilon)\)의 수렴 속도를 갖는다.

Projected gradient descent

\(I_C(x)\)가 closed convex set \(C ∈ \mathbb{R}^n\)의 Indicator 함수일 때 \(g(x)\)를 집합 \(C\)에 대해 최소화 하는 문제는 다음과 같이 재정의하여 표현할 수 있다. (참고로 \(C\)가 closed set이어야 하는 이유는 closed set이어야 projection이 잘 정의될 수 있기 때문이다.)

\[\min_{x \in C} g(x) \iff \min_x g(x) + I_C(x)\]

\[I_C(x) = \begin{cases} 0, & x \in C \\ \infty, & x \notin C \end{cases}\]

이때 proximal mapping은 다음과 같이 정의된다.

\[\begin{align} \text{prox}_t(x) &= \underset{z}{\text{argmin}} \frac{1}{2t} \lVert x−z \rVert_2^2 + I_C(z) \\ & = \underset{z \in C}{\text{argmin}} \lVert x−z \rVert_2^2 \end{align}\]

결과적으로 proximal mapping \(\text{prox}_t(x) = P_C(x)\)는 \(C\)에 대한 사영 오퍼레이터 (projection operator)라고 할 수 있다.

Proximal gradient 업데이트 단계는: \(x^+ = P_C (x−t \nabla g(x) )\)와 같이 정의된다. 풀어서 설명하면 gradient descent로 업데이트를 수행 한 후 \(C\)에 대해 사영(project)을 수행한다고 보면 된다.

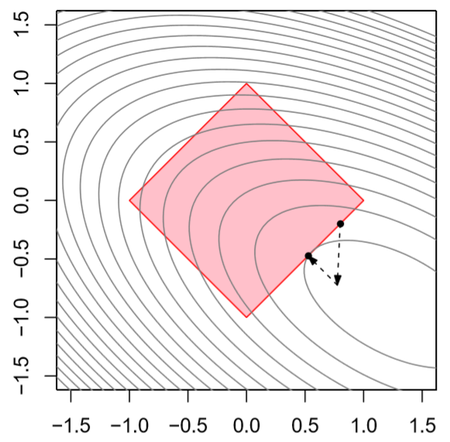
아래 그림을 보면 분홍색 사각형이 feasible set \(C\)이며 현재 위치는 사각형 아래의 두 점 중 윗쪽 점이다. Gradient descent로 한 스텝을 이동하게 되면 \(C\)를 벗어나게 되므로 다시 \(C\)에 대해 사영을 해서 feasible set 안쪽으로 들어오게 됨을 알 수 있다.

Proximal minimization algorithm

다음가 같이 Convex \(h\)를 최소화하는 문제를 고려해보자. 이때, \(h\)는 미분가능할 필요는 없으며 \(g(x) = 0\)이다.

\begin{align} \min_x h(x) \end{align}

Proximal mapping은 다음과 같이 정의된다.

\[\begin{align} x^{(k)} &= \text{prox}_{t_k} \big(x^{(k-1)} - t_k \nabla g ( x^{(k-1)} ) \big) , \qquad k = 1, 2, 3, ... \\ &= \text{prox}_{t_k} \big(x^{(k-1)} \big) , \qquad \qquad \qquad \qquad \; k = 1, 2, 3, ... \\ \end{align}\]

따라서 proximal gradient 업데이트 단계는 다음과 같다:

\[x^+ = \underset{z}{\text{argmin}} \frac{1}{2t} \lVert x−z \rVert_2^2 + h(z)\]

이와 같이 \(g\)는 \(0\)이고 \(h\)로만 정의되는 proximal gradient 방법을 proximal minimization algorithm(PMA) 라고 한다. 이 방법은 subgradient보다는 빠르지만 proximal mapping이 closed form이 아니면 구현이 불가능하다.

What happens if we can’t evaluate prox?

이론적으로는 \(f = g + h\)에 대해 proximal gradient을 적용할 때는 prox 함수가 정확히 계산될 수 있다고 가정한다. 즉, proximal mapping을 통해 최소값을 정확히 구할 수 있다고 가정한다.

\[\text{prox}_t(x )= \underset{z}{\text{argmin}} \frac{1}{2t} \lVert x−z \rVert_2^2 + h(z)\]

일반적으로 최소값을 근사할 경우 어떤 일이 일어나는지는 정확히 알 수 없다. 하지만 prox operator를 근사할 때 에러를 정확히 제어 할 수 있다면 원래의 수렴 속도를 가질 수 있음이 밝혀져 있다. (Schmidt et al. (2011), Convergence rates of inexact proximal-gradient methods for convex optimization”)

실제 prox가 근사적으로 계산될 수 있다면 높은 정확도로 수행될 것이다.