08-01-07 Example: Intersection of sets

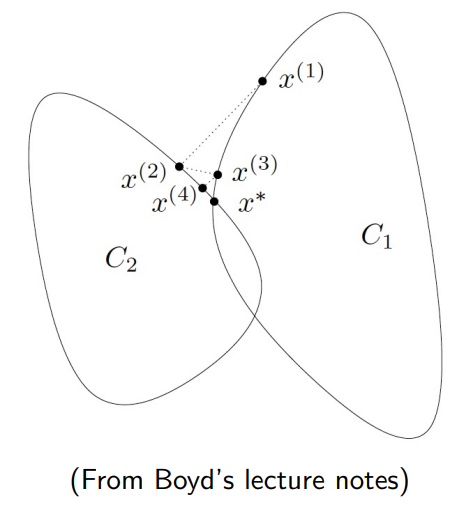
닫힌 컨벡스 집합(closed convex set)들의 교차점을 찾고 싶다고 하자.

우선, 임의의 점 \(x\)로 부터 집합 \(C_i\)까지의 거리를 나타내는 \(f_i(x)\)와 점 \(x\)에서 모든 집합 \(C_i, i=1,...,m\)에 대해 가장 먼 거리를 나타내는 \(f\)를 정의해보자.

\[\begin{align} f_i(x) & = \mathbb{dist}(x, C_i), i=1,...,m \\ f(x) & = \max_{1,...,m}\text{ }f_i(x) \end{align}\]

위의 두 함수를 이용하면 다음과 같이 컨벡스 집합들의 교차점을 찾는 최적화 문제로 정의할 수 있다.

\[\begin{align} min_{x}\text{ }f(x) \end{align}\]

컨벡스 집합의 교차점을 구하는 문제는 임의의 점 \(x\)와 가장 먼 컨벡스 집합 \(C_i\)의 거리 \(f_i(x)\)를 최소화하는 \(x\)를 구하는 문제로 바뀐다. 이때, 위 문제의 목적 함수인 \(f(x)\)는 컨벡스이다. 만약 모든 집합의 동시적인 교차점이 존재한다면 \(f^* = 0\)이 될 것이고 optimal point는 \(x^* \in C_1 \cap C_2 \cap ... \cap C_m\)로 표현할 수 있다.

Gradient of distance function

이전 장에서 컨벡스 집합과의 거리를 \(dist(x, C_i) = \min_{y \in C} \lVert y-x \lVert _2\)로 정의했고 이 함수의 gradient는 다음과 같음을 보였다.

\[\begin{align} \partial dist(x,C) = \frac{x-P_C(x)}{ \Vert x-P_C(x) \Vert_2} \end{align}\]

여기서 \(P_C(x)\)는 점 \(x\)에서 집합 \(C\)으로의 projection이다.

Subdifferential of finite pointwise maximum

Finite pointwise maximum 함수 \(f(x)=max_{i=1,...,m}\text{ }f_i(x)\)에 대한 subdifferential은 다음과 같이 정의 된다.

\[\begin{align} \partial f(x) = \text{conv}\left(\bigcup_{i:f_i(x)=f(x)} \partial f_i(x)\right) \end{align}\]

즉, \(x\)의 subdifferential은 그 지점의 모든 subdifferential \(\partial f_i(x), i=1,...,m\)의 합집합에 대한 convex hull로 정의된다.

만약 \(f_i(x) = f(x)\) 이고 \(g_i \in \partial f_i(x)\)이라면 \(g_i \in \partial f(x)\)이다.

Deriving subgradient updating steps

이전 장에서 보았던 \(dist(x, C_i)\)는 다음과 같은 subgradient를 가진다.

\(Recall:\) \(\begin{align} g_i = \nabla f_i(x) = \frac{x-P_{C_i}(x)}{ \Vert x-P_{C_i}(x) \Vert_2} \end{align}\)

만약 컨벡스 집합의 교차점이 있다면 우리는 \(f^*=0\)임을 바로 알 수 있기에 Polyak step sizes를 사용할 수 있다. 위 subgradient 수식을 보면 \(x-P_{c_i}(x)\)가 정규화된 형태이므로 \(\Vert g \Vert_2^{2}=1\)이다. 결국 Polyak step size \(t_k = \{\frac{f^{(k-1)}-f^*}{ \Vert g^{(k-1)} \Vert_2^{2}}\}\)에 우리가 알고 있는 값을 대입하면 다음과 같은 subgradient method 공식을 도출할 수 있다.

\[\begin{align} x^{(k)} & = x^{(k-1)} - t_{k}⋅g_{k-1} \\ & = x^{(k-1)} - \frac{f^{(k-1)}-f^*}{ \Vert g^{(k-1)} \Vert_2^{2}} \frac{x^{(k-1)}-P_{C_i}(x)}{ \Vert x^{(k-1)}-P_{C_i}(x) \Vert_2} \\ & = x^{(k-1)} - f(x^{k-1}) \frac{x^{(k-1)}-P_{C_i}(x)}{ \Vert x^{(k-1)}-P_{C_i}(x) \Vert_2} \end{align}\]

여기서 Polyak size인 \(f(x^{(k-1)})\)는 \(dist(x_i^{(k-1)}, C_i) = \Vert x^{(k-1)}-P_{C_i}(x) \Vert_2\) 이므로 subgradient method는 아래와 같이 정리된다.

\[\begin{align} x^{(k)} = P_{C_i}(x^{(k-1)}) \end{align}\]

이 문제는 그림으로 표현하면 각 스텝에서 가장 가까운 컨벡스 함수에 projection을 반복하는 형태이다.