08-01-05 Example: Regularized Logistic Regression

만약 \(i=1,...,n\)에 대해서 \((x_i,y_i) \in R^p ×\){\(0, 1\)}가 주어졌을때, logistic regression loss는 다음과 같다.

\begin{align} f(\beta) = \sum_{i=1}^n\big(-y_ix_i^T\beta + log(1+exp(x_i^T\beta))\big) \end{align}

이 함수는 linear 함수와 log-sum-exp 함수의 finite sum의 형태로서 미분 가능한 컨벡스 함수이다.

이때 우리가 \(\beta\)에 대한 regularization problem은 다음과 같이 정리된다.

\begin{align} min_{\beta} \text{ } f(\beta) + \lambda ⋅ P(\beta) \end{align}

여기서 \(P(\beta)가 \Vert \beta \Vert _2^2\)(ridge penalty) 또는 \(\Vert \beta \Vert _1\)(lasso penalty)로 정의된다고 해보자.

Ridge penalty를 적용한 loss 함수는 여전히 미분 가능한 컨벡스 함수이지만 lasso penalty를 적용한 loss 함수는 미분 불가능한 컨벡스 함수가 된다.

이러한 두 loss 함수에 대해 gradient descent for ridge와 subgradient method for lasso를 적용하여 시행 횟수 \(k\)에 대한 objective function의 값을 출력해보면 두 방정식의 수렴 특징을 관찰할 수 있다.

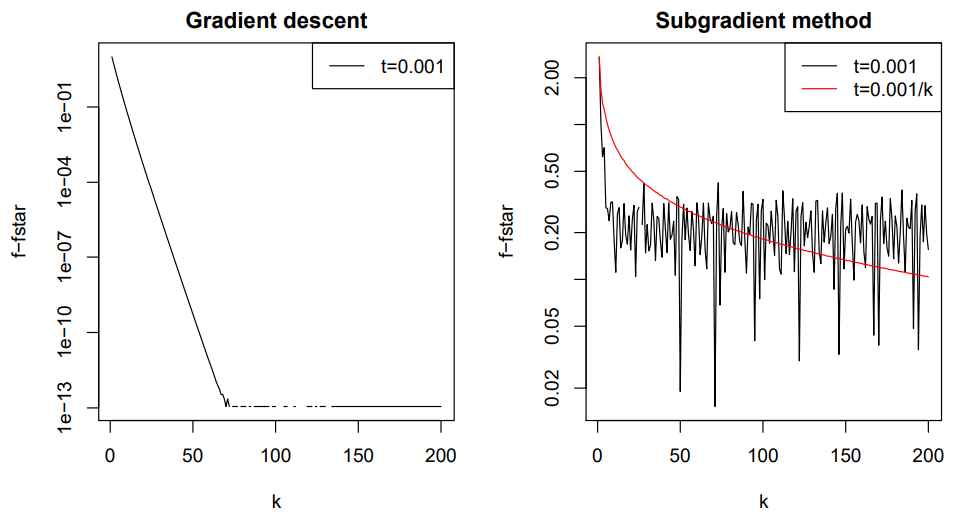
위 실험은 gradient descent가 subgradient method보다 수렴속도가 훨씬 빠르다는 것을 보여준다.