07-03-04 Example: Soft-Thresholding

\(X=I\)인 좀 더 간단한 lasso 문제는 아래와 같다.

\begin{equation} \min_{\beta} \frac{1}{2} \vert \vert y-\beta \vert \vert _2^2 + \lambda \vert \vert \beta \vert \vert _1 \end{equation}

앞선 예제로부터 subgradient 최적 조건은 아래와 같게 된다.

\[\begin{cases} y_i-\beta_i = \lambda \cdot \text{sign}(\beta_i) &\text{if } \beta_i \neq 0 \\ \vert y_i-\beta_i \vert \leq \lambda &\text{if } \beta_i = 0 \end{cases}\]

위 조건으로부터 \(\beta = S_{\lambda}(y)\)의 해를 구할 수 있다. 이때,

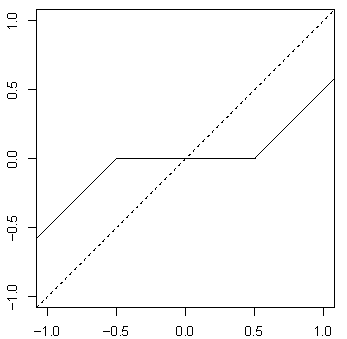
\[[S_{\lambda}(y)]_{i} = \begin{cases} y_i - \lambda &\text{if }y_i > \lambda \\ 0 &\text{if }-\lambda \leq y_i \leq \lambda, \quad \quad i \in \{1,2,\dots,n \} \\ y_i + \lambda &\text{if } y_i < -\lambda \end{cases}\]

여기서 \(S_{\lambda}\)를 soft-thresholding operator라 부른다.