07-01 Subgradient

Subgradient

어떤 볼록함수(convex function) \(f:\mathbb{R}^n \to \mathbb{R}\)의 subgradient는 다음의 조건을 만족하는 \(g \in \mathbb{R}^n\)로 정의된다.

\[\begin{equation}\label{subgradient} f(y) \geq f(x) + g^T(y-x), \text{ for all y} \end{equation}\]

위에서 정의된 subgradient는

• 미분가능한 볼록함수의 gradient를 미분가능하지 않은 볼록함수에도 적용할 수 있도록 일반화한 것이며,
• 볼록함수에 대해서는 항상 존재하는 값으로서, 만약 \(f\)가 \(x\)에서 미분가능하면 \(\nabla f(x)\)를 유일하게 갖게된다.
• 비볼록함수(non-convex function) 에 대해서도 동일하게 subgradient가 구해질 수 있으나 이 때는 함수에 따라서 값이 존재하지 않을 수 있다.

다음은 몇 가지 함수들에 대한 subgradient의 예를 보여준다.

Example1

$$f:\mathbb{R} \to \mathbb{R}, f(x) = \vert x \vert $$

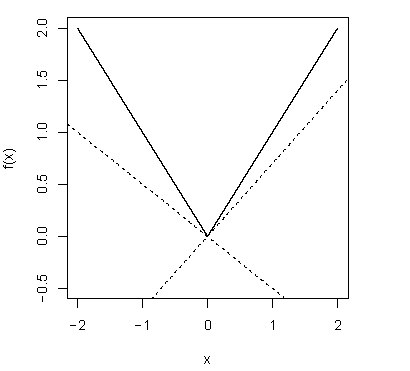
• \(x \neq 0\)에 대해, \(\vert y \vert \geq \vert x \vert + g^T(y-x)\)를 만족해야 한다. 즉,

\(\vert y \vert -g^Ty \geq \vert x \vert -g^Tx\). \(\vert x \vert -g^Tx = 0\)이면 즉, \(g=\text{sign}(x)\)이면, 모든 \(y\)에 대해 항상 만족됨. 따라서, \(g=\text{sign}(x)\) [(Wikipedia) Sign function]

• \(x=0\)에 대해, \(\vert y \vert \geq g^Ty\)를 만족해야 함. 따라서, \(g \in [-1,1]\)

Example2

$$f:\mathbb{R}^n \to \mathbb{R}, f(x) = \vert \vert x \vert \vert _1$$

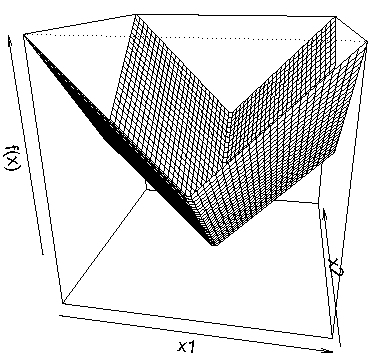
한 점 \(x=(x_1,x_2,\dots,x_n)\)에서,

• \(x_i \neq 0, i \in \{1,2,\dots,n\}\)에 대해, \(x_i\)에서 미분가능하므로 \(g_i=\text{sign}(x_i)\)

• \(x_i=0, i \in \{1,2,\dots,n\}\)에 대해, \(g_i \in [-1,1]\)

Example3

$$f:\mathbb{R}^n \to \mathbb{R}, f(x) = \vert \vert x \vert \vert _2$$

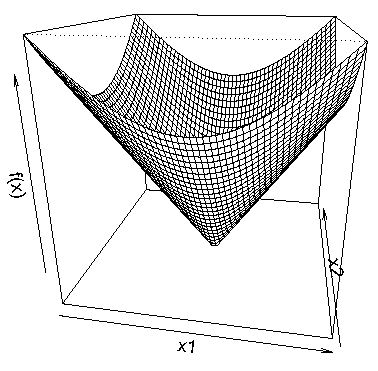
• \(x \neq 0\)에 대해, 미분가능하므로 \(g=\nabla \sqrt{x^Tx} = \frac{1}{2}(x^Tx)^{-\frac{1}{2}} (2x) = \frac{x}{ \vert \vert x \vert \vert _2}\)

• \(x=0\)에 대해, \(\vert \vert y \vert \vert _2 \geq g^Ty \Longrightarrow \vert \vert y \vert \vert _2 \geq \vert \vert g \vert \vert _2 \vert \vert y \vert \vert _2 \cos \theta\). 따라서 \(g \in \{z: \vert \vert z \vert \vert _2 \leq 1 \}\)

Example4

\(f(x) = \max f_1(x),f_2(x)\), 이때, \(f_1,f_2:\mathbb{R}^n \to \mathbb{R}\)이며, 모두 볼록함수이고 미분가능.

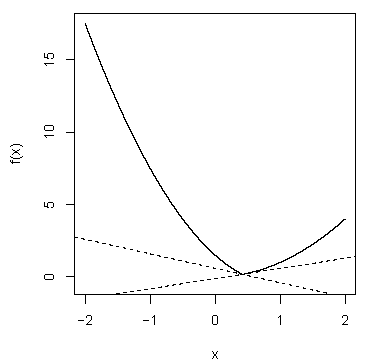
• \(f_1(x) > f_2(x)\)에 대해, \(g = \nabla f_1(x)\)

• \(f_1(x) < f_2(x)\)에 대해, \(g = \nabla f_2(x)\)

• \(f_1(x) = f_2(x)\)에 대해, \(g \in \{\theta_1 \nabla f_1(x) + \theta_2 \nabla f_2(x): \theta_1 + \theta_2 = 1, \theta_1 \geq 0, \theta_2 \geq 0 \}\)