모두를 위한 컨벡스 최적화

06-04 Gradient boosting

Gradient boosting

Gradient boosting은 여러 트리로 구성된 앙상블 모델로 결과를 예측하려고 할 때, gradient descent를 이용해서 순차적으로 트리를 만들어가며 이전 트리의 오차를 보완하는 방식으로 boosting을 하는 방법이다. Gradient Boosting은 회귀와 분류에 모두 사용할 수 있다.

[참고] Functional gradient descent 알고리즘

Gradient boosting은 Llew Mason, Jonathan Baxter, Peter Bartlett and Marcus Frean에 의해 functional gradient descent 알고리즘으로 소개되었다. Functional gradient descent 알고리즘은 함수 공간에 대해서 loss function을 최적화하는 알고리즘으로 gradient의 음수 방향을 갖는 함수를 반복적으로 선택함으로써 gradient decent를 수행한다.

[참고] Boosting과 Bagging

Boosting은 weak learner를 순차적으로 생성해서 결과를 예측하는 앙상블 기법이다. 이전 단계의 learner가 잘못 예측한 데이터를 다음 단계의 learner가 학습해서 순차적으로 생성된 learner들의 결과를 취합해서 최종 결과로 만든다.

Bagging은 weak learner를 서로 독립적으로 생성해서 결과를 예측하는 앙상블 기법이다. 따라서, 각 learner들은 병렬적으로 실행이 되고 그 결과를 취합해서 최종 결과로 만든다.

트리로 구성된 앙상블 모델이 있고 분류에 사용한다고 가정해 보자. 이 모델은 관측값과의 오차가 최소화 되는 결과를 예측하고자 할 것이다. 관측값은 \(y_i\), \(i=1,\dots,n\)로, 입력 데이터는 \(x_i, i=1,\dots,n\)로, 예측값은 \(u_i\), \(i=1,\dots,n\)라고 하자.

아래 그림과 같이 앙상블에 소속된 각 트리는 \(x_i \in R^p\)를 입력으로 받아 트리의 노드에 있는 분기 조건에 따라 결과를 출력하게 된다.

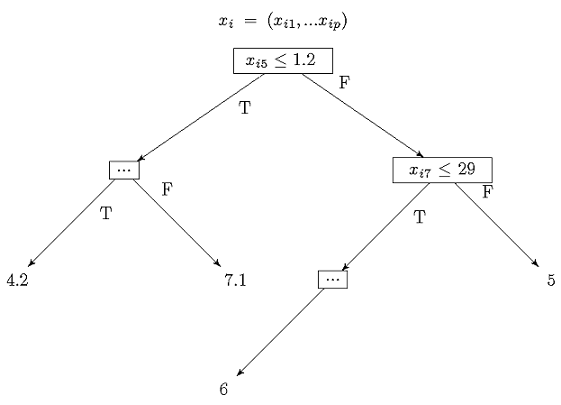
tree_O9zyAlk

$$\text{[Fig 1] Example of Tree }T_j\text{ [3]}$$

앙상블 모델의 예측값 \(u_i\)는 각 트리의 결과를 가중 합산해서 계산할 수 있다. (여기서 \(T_j(x_i)\)는 트리 \(j\)가 \(x_i\)를 입력으로 받아 출력한 결과이다.)

\[\begin{equation} u_i = \sum_{j=1}^M \beta_j T_j(x_i) \end{equation}\]

Loss 함수의 경우 관측값과 예측값의 오차가 최소화되도록 오차 제곱의 합 형태인 \(L=(y_i,u_i)=(y_i - u_i)^2\)로 정의할 수 있다.

\[\begin{equation} \min_{\beta} \sum_{i=1}^n L\left(y_i, \sum_{j=1}^M \beta_j T_j(x_i)\right) \end{equation}\]

일반적으로 앙상블 모델에서 트리 구성을 할 때는 고정 depth를 갖는 작은 트리를 아주 여러개 만든다. 왜냐하면 트리를 작게 하면 메모리도 적게 사용하고 예측도 빠르게 할 수 으며 트리의 개수가 많아질 수록 앙상블의 성능은 좋아지게 되기 때문이다. 일반적으로 트리의 depth는 5이하로 고정한다.

따라서, 이 문제의 경우 각 트리에 정의된 노드 조건이 매우 다양하고 아주 많은 트리의 결과가 선형 결합되기 때문에 트리 공간이 상당히 크다. 따라서, 최적화를 하기가 매우 어려운 문제라고 할 수 있다.

이 문제를 풀려면 최적화 문제를 좀 더 쉬운 문제로 바꿔야 한다. 원래 최적화 문제는 Loss 함수를 최소화하는 \(M\)개의 가중치 \(\beta_j\)를 찾는 문제이다. 이 문제를 예측값 \(u\)에 대한 함수 \(f(u)\)를 최소화 문제 \(\min_{u} f(u)\)로 생각해 보자. 함수 \(f(u)\)가 Loss 함수 \(L(y,u)\)라고 하면 Loss 함수를 최소화 하는 \(u\)를 찾는 것이 쉽게 재정의된 문제라고 할 수 있다. (여기서 \(n\)은 데이터 개수이다.)

Gradient boosting는 \(\min_{u} f(u)\)로 재정의된 최소화 문제를 gradient descent를 이용해서 푸는 기법을 말한다.

Algorithm

Gradient boosting 알고리즘은 \(\min_u L(y, u)\)의 최적해 \(u^*\)를 찾기 위해 다음과 같은 방식으로 gradient descent를 수행한다.

  1. 초기 값은 임의의 트리의 결과 값으로 \(u^{(0)}=T_0\)와 같이 설정한다. 그리고, 다음의 2~4 단계를 반복한다.

  2. \(n\)개의 데이터의 가장 최근의 예측값인 \(u^{(k-1)}\)에 대한 음수 gradient를 계산한다.
    \[\begin{equation} d_i = - \left . \left[ \frac{\partial L(y_i,u_i)}{\partial u_i} \right] \right|_{u_i = u_i^{(k-1)}}, i=1,\dots,n \end{equation}\]
  3. \(n\)개 데이터에 대한 gradient \(d_i\)와 트리의 결과 \(T(x_i)\)가 가장 비슷한 트리 \(T_k\)를 찾는다.
    \[\begin{equation} \min_{\text{trees } T} \sum_{i=1}^n (d_i-T(x_i))^2 \end{equation}\]
  4. Step size \(a_k\)를 계산하고 위에서 찾은 \(T_k\)를 이용하여 예측값을 업데이트한다.
    \[u^{(k)}=u^{(k-1)} + \alpha_k T_k\]

이 알고리즘은 gradient descent로 최적해 \(u^*\)를 찾기 위해 \(u\)에 대한 gradient \(d\)를 구하고, \(d\)에 가장 가까운 \(T_k\)를 찾아서 업데이트 식에 gradient 대신 \(T_k\)를 대입해서 다음 위치를 구한다.

이렇게 해서 구한 최종 예측값 \(u^*\)는 앞에서 정의했던 트리 결과의 가중 합산과 동일해짐을 알 수 있다. (즉, 재귀식 형태의 업데이트 식 \(u^{(k)}=u^{(k-1)} + \alpha_k T_k\)을 \(k=0\)까지 풀어보면 \(u^* = \sum_{k=1}^n \alpha_k T_k\)가 되어 트리 결과의 가중 합산 형태로 만들 수 있다. )