06-03-04 Convergence analysis under strong convexity
함수 \(f\)가 다음 조건을 만족하게 되면 strongly convex하다고 할 수 있다. (단, \(f\)는 2번 미분가능해야 하며 상수 \(m\)은 양수이어야 한다.)
\[\begin{align} f(y) & \ge f(x) + \nabla f(x)^T(y−x) + \frac{m}{2} \lVert y−x \rVert_2^2, \space \forall x, y \end{align}\]
이 조건에서 함수 \(f\)가 2차 lower bound를 갖는다는 것을 알 수 있다. 이때, 2차 항의 계수는 상수 \(m\)으로 결정된다. (상수 m은 함수 \(f\)의 2차 미분 계수인 hessian의 최소 eigenvalue이다.)
다음과 같이 함수 \(g\)가 convex라면 함수 \(f\)를 strong-convex function이라고 할 수 있다. 이 조건은 위의 조건과 동치이다.
\[\begin{align} g(x) & = f(x) − \frac{m}{2} \lVert x \rVert_2^2 \space \space \text{is convex} , \space \forall x \space \text{and} \space m \gt 0 \\\ \end{align}\]
Convergence Theorem
Lipschitz continuous와 strong convexity 가정에 의하여 다음의 theorem이 성립한다. (이때, 상수 \(L\)은 Lipschitz constant이며 상수 \(m\)은 strong convexity를 만족할 때 quadratic term의 계수이다.)
Gradient descent는 fixed step size(\(t ≤ 2/(m + L)\)) 또는 backtracking line search에 대해 다음 식을 만족한다. \(\begin{align} f(x^{(k)}) − f^{\star} ≤ c^k \frac{L}{2} \lVert x^{(0)} −x^{\star} \rVert_2^2, \text{where} \space c = (1 - \frac{m}{L}), \space 0 \lt c \lt 1 \end{align}\)
Proof
\(\nabla f\)는 Lipschitz continuous하며 \(f\)는 Lipschitz constant \(L\)을 계수로 하는 2차 항으로 된 quadratic upper bound를 갖는다. (Upper bound의 증명은 06-03-02 절을 참조)
\[\begin{align} f(y) \le f(x) + \nabla f(x)^T (y-x) + \frac{L}{2} \lVert y - x \rVert^2_2 \space \space \forall x, y \end{align}\]
Gradient descent를 현재 위치 \(x\)에서 다음 위치 \(x^+ = x - t \nabla f(x)\)로 진행한다고 해보자. 위의 식에서 \(y = x^+\)라고 하고 전개해보자.
\[\begin{align} f(x^+) & \le f(x) + \nabla f(x)^T (x^+ - x) + \frac{L}{2} \lVert x^+ - x \rVert^2_2 \\\ & = (x) + \nabla f(x)^T (x - t \nabla f(x) - x) + \frac{L}{2} \lVert x - t \nabla f(x) - x \rVert^2_2 \\\ & = f(x) - t \nabla f(x)^T (\nabla f(x)) + \frac{L}{2} \lVert t \nabla f(x) \rVert^2_2 \\\ & = f(x) - t \lVert \nabla f(x)) \rVert^2_2 + \frac{Lt^2}{2} \lVert \nabla f(x) \rVert^2_2 \\\ \end{align}\]
이 식을 \(t\)에 대해 미분을 해보면 \(t = 1/L\)일때 최소가 된다. 따라서, 이 식에 \(t = 1/L\)을 대입하면 다음 식을 얻게 된다.
\[\begin{align} f(x^+) & \le f(x) - \frac{1}{2L} \lVert \nabla f(x) \rVert^2_2 \\\ \end{align}\]
양변에서 \(f(x^{*})\)을 빼보자.
\[\begin{align} f(x^+) - f(x^{*}) & \le f(x) - f(x^{*}) - \frac{1}{2L} \lVert \nabla f(x) \rVert^2_2 \\\ \end{align}\]
Gradient Descent는 아래 조건을 만족하므로 이 조건을 \(2m(f(x) - f(x^{*})) \le \lVert \nabla f(x) \rVert^2_2\)와 같이 정리해서 위의 식에 대입한다.
\[\begin{align} f(x) - f(x^{*}) \le \frac{1}{2m} \lVert \nabla f(x) \rVert^2_2 \\\ \end{align}\]
그러면 다음 식과 같이 정리가 되며 이때 \(c = (1 - \frac{m}{L})\)라고 하자.
\[\begin{align} f(x^+) - f(x^{*}) & \le f(x) - f(x^{*}) - \frac{m}{L} ( f(x) - f(x^{*}) ) \\\ & = (1 - \frac{m}{L} ) ( f(x) - f(x^{*}) ) \\\ & = c ( f(x) - f(x^{*}) ) \\\ \end{align}\]
이 식을 반복하게 되면 다음의 관계를 얻을 수 있다.
\[\begin{align} f(x^{(k)}) - f(x^{*}) & \le c^k ( f(x^{(0)}) - f(x^{*}) ) \\\ \end{align}\]
다음 함수의 Taylor 식에 \(y = x^{(0)}\)을 \(x = x^{*}\)을 대입해 보자.
\[\begin{align} f(y) \le f(x) + \nabla f(x)^T (y-x) + \frac{L}{2} \lVert y - x \rVert^2_2 \space \space \forall x, y \end{align}\]
함수가 Convex이므로 \(\nabla f(x^{*})\)는 0이 되며 식은 다음과 같이 정리된다.
\[\begin{align} f(x^{(0)}) & \le f(x^{*}) + \nabla f(x^{*})^T (x^{(0)}- x^{*} ) + \frac{L}{2} \lVert x^{(0)} - x^{*} \rVert^2_2 \\\\ & = f(x^{*}) + \frac{L}{2} \lVert x^{(0)} - x^{*} \rVert^2_2 \\\\ \end{align}\]
\(f(x^{*})\)를 좌변으로 넘기면 다음과 같이 정리된다.
\[\begin{align} f(x^{(0)}) - f(x^{*}) & \le \frac{L}{2} \lVert x^{(0)} - x^{*} \rVert^2_2 \\\\ \end{align}\]
이 식를 위의 식에 대입해 보자.
\[\begin{align} f(x^{(k)}) - f(x^{*}) & \le c^k \frac{L}{2} \lVert x^{(0)} - x^{*} \rVert^2_2 \\\ \end{align}\]
이로써 Strong Convexity를 만족할 때 Gradient descent의 Convergence Theorem이 증명되었다.
Linear convergence
\(f\)가 strongly convex일 경우 convergence rate는 (\(O(c^k)\))가 되어 기하급수적으로 빨라진다. 또한, \(f(x^{(k)}) - f^{*} \le \epsilon\)라면 \(O(\log(1/\epsilon)\)의 반복이 필요하다. (\(f\)가 strongly convex가 아닐 경우 \(O(1/\epsilon)\) 반복이 필요했다.)
수렴 속도 \(O(c^k)\)는 아래 그림과 같이 semi-log plot에서 선형처럼 보이므로 선형적 수렴(linear convergence)이라고도 부른다.
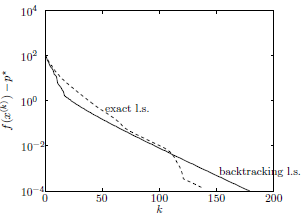
\(O(c^k)\)에서 상수 c는 \(1 - \frac{m}{L}\)로 condition number \(L/m\)에 따라 달라진다. Condition number가 커질수록 속도가 느려진다. (Condition number = largest eigenvalue / smallest eigenvalue이다.)