06-02-02 Backtracking line search
Gradient descent에서 고정 step size를 사용하게 되면 진행 속도가 항상 동일하기 때문에, 경사가 가파른 구간에서는 최적점을 지나쳐서 진동할 수 있으며 경사가 평평한 구간에서는 진행이 느려질 수가 있다. 따라서, 곡면의 특성에 맞춰 속도를 조절하면서 진행해야 수렴도 보장되고 수렴 속도도 높아진다. 이와 같이 곡면의 특성에 맞춰 step size를 적응적으로 선택하는 방법 중 하나가 backtracking line search이다.
Backtracking line search 방법이란?
이 방법은 다음 위치를 결정할 때 현재 위치에서 한 step을 가보고 너무 많이 갔다고 판단하면 다시 되돌아 오는 방법이다. 다음 그림은 backtracking line search로 다음 step을 결정하는 방식을 보여준다.
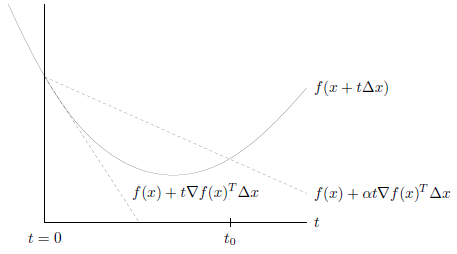
곡면 \(f\)에서 탐색 범위는 직선으로 제한된다. 아래쪽 점선은 현재 위치 \(x\)에서 접선 방향으로 한 step 간 경우이다. 이 경우 \(f\)가 항상 직선보다 위쪽에 있으므로 많이 간 것인지 적당히 간 것인지 자세히 판단하기가 어렵다.
Backtracking line search에서는 위쪽 점선을 사용한다. 위쪽 점선은 접선의 기울기에 \(\alpha\)를 곱한 방향으로 한 step 간 경우이다. 이때, 직선은 항상 \(f(x+t\Delta x)\)와 교차하므로, 한 step 간 지점에서 \(f(x+t\Delta x)\)의 위치가 점선 위에 있으면 너무 많이 갔다고 판단하고 \(f(x+t\Delta x)\)의 위치가 점선 아래에 있으면 적당히 잘 갔다고 판단한다.
너무 많이 간 경우에는 되돌아 오기 위해 \(t\)를 줄이고 \(f\)가 점선 아래로 오게 만든다. 이때 \(t\)의 위치는 \(0 \le t \le t_0\)구간 안으로 들어온다.
Backtracking line search 알고리즘
이 내용을 알고리즘으로 정리하면 다음과 같다. (단, \(\Delta x = - \nabla f(x)\))
- 파라미터를 초기화한다. (\(0 \lt \beta \lt 1\), \(0 \lt \alpha \le 1/2\))
- 각 반복에서 \(t = t_{init}\)로 초기화 한다. (\(t_{init} = 1\))
- 조건 \(f(x - t \nabla f(x) ) \gt f(x) - \alpha t \lVert \nabla f(x) \rVert_2^2\)을 만족하면 \(t = \beta t\)로 줄인다. 이 조건이 만족되는 동안 3을 반복한다.
- Gradient descent update \(x^+ = x - t \nabla f(x)\)를 실행한다.
- 종료 조건을 만족하지 않으면 2로 간다.
Backtracking line search은 단순하지만 매우 잘 실행된다. 파라미터 \(\alpha\)는 다음 step의 방향을 결정하며, \(\beta\)는 다음 step을 얼마나 되돌아 올 지 결정한다. \(\beta\) 값이 작으면 크게 되돌아 오기 때문에 3번 반복 회수는 적어지지만 step size가 작아져서 한번에 멀리 가지는 못한다. 실제 파라미터 선정은 알고리즘의 성능에 크게 영향을 주지 않으며, 대부분 \(\alpha = 1/2\)로 \(\beta\)는 1에 가까운 값으로 선정한다.
Backtracking line search 수렴 예시
Backtracking 방식으로 adaptive하게 step size를 선정하게 되면 fixed step size로 100 step만에 수렴했던 예제가 12 step만에 수렴한다 (\(\alpha = \beta = 1/2\)). 내부 backtracking step까지 포함해도 총 40 step만에 수렴한다.
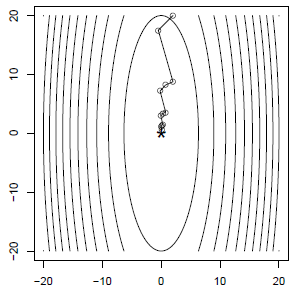
The intuition of Backtracking line search
함수 \(f\)에 대한 quadratic approximator는 다음과 같이 정의된다. \(f(y) \approx f(x) + \nabla f(x)^T(y-x) + \frac{1}{2t} \vert \vert y - x \vert \vert_2^2\) 이때, \(y = x - t \nabla f(x)\)라 하면, \(\begin{align} f(x - t \nabla f(x)) &\approx f(x) + \nabla f(x)^T (x - t \nabla f(x) - x) + \frac{1}{2t} \vert \vert x - t \nabla f(x) - x \vert \vert_2^2 \\ &= f(x) - t \vert \vert \nabla f(x) \vert \vert_2^2 + \frac{1}{2t} \vert \vert -t \nabla f(x) \vert \vert_2^2 \\ &= f(x) - t \vert \vert \nabla f(x) \vert \vert_2^2 + \frac{1}{2}t \vert \vert \nabla f(x) \vert \vert_2^2 \\ &= f(x) - \frac{1}{2}t \vert \vert \nabla f(x) \vert \vert_2^2 \end{align}\)
즉, \(f(x) - \frac{1}{2}t \vert \vert \nabla f(x) \vert \vert_2^2\)는 \(f(x - t \nabla f(x))\)의 quadratic approximator이다. 이 두 함수 사이의 부등호 방향에 따른 기하학적인 의미를 살펴보자. (빨간선: \(f(x - t \nabla f(x))\), 파란선: \(f(x) - \frac{1}{2}t \vert \vert \nabla f(x) \vert \vert_2^2\))
(1) \(f(x - t \nabla f(x)) < f(x) - \frac{1}{2}t \vert \vert \nabla f(x) \vert \vert_2^2\)
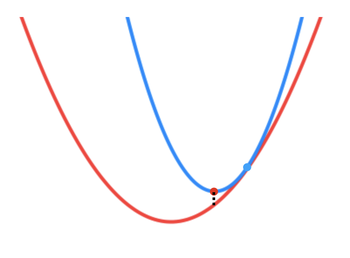
Quadratic approximator가 \(x - t \nabla f(x)\)에서 더 위에 위치하는 형태이다. Quadratic approximator의 solution에 접근하면 \(f(x)\)의 solution에 더 가까이 접근할 수 있음이 보장된다.
(2) \(f(x - t \nabla f(x)) > f(x) - \frac{1}{2}t \vert \vert \nabla f(x) \vert \vert_2^2\)
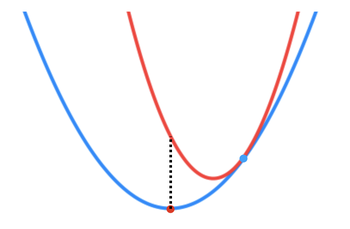
(1)의 경우와는 반대되는 양상을 보인다. Quadratic approximator의 solution을 통해 \(f(x)\)의 solution에 더욱 접근할 수 있음이 보장되지 않는다.
결론: 매 스텝에서 t 값을 잘 조정하여 항상 \(f(x - t \nabla f(x)) \leq f(x) - \frac{1}{2}t \vert \vert \nabla f(x) \vert \vert_2^2\)를 만족하도록 하면 훨씬 효과적으로 \(f(x)\)의 solution에 접근할 수 있다.