06-01 Gradient Descent
Gradient descent는 제약조건이 없는 convex이고 differentiable한 function의 최적화 문제를 풀기위한 가장 단순한 알고리즘이다.
\(\min_x f(x),\) \(f\) : differentiable with \(dom(f) = R^n\).
참고로, optimal value는 \(f^{*} = min_x f(x)\)로 optimal은 \(x^{*}\)로 표기한다.
Gradient decent method
Gradient descent는 초기 점 \(x^{(0)} \in R^n\)을 선택하고 다음 식을 반복적으로 실행해서 임의의 조건을 만족하면 종료하게 된다.
\(x^{(k)} = x^{(k-1)} - t_k \nabla f(x^{(k-1)}), k = 1, 2, 3, . . .\), \(t_k \gt 0\)
이를 pseudocode로 정리해보면 다음과 같다.
give a starting point x , \(x \in\) dom \(f\)
repeat
- Determine a descent direction \(\Delta x = -\nabla f(x)\).
- Line Search. Choose a step size \(t \gt 0\).
- Update \(x = x + t \Delta x\).
until stopping criteion is satisfied
Examples
다음 그림에는 함수 \(f\)가 convex function일 때 gradient descent를 수행을 보여주고 있다. 이 경우, local minimum = global minimum에 도달할 수 있게 된다.
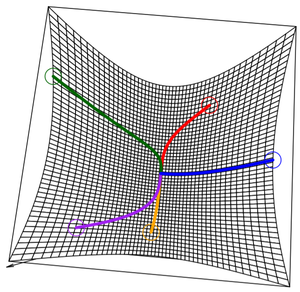
반면 다음 그림에는 함수 \(f\)가 non-convex function일 때 gradient descent를 수행을 보여주고 있다. 이 경우 초기점이 어느 곳에 위치하느냐에 따라서 각각 다른 곳에 존재하는 local minimum으로 수렴한다.
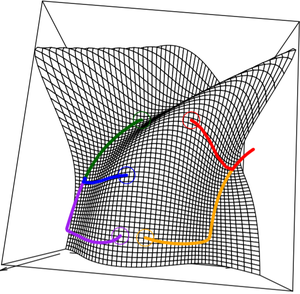
Gradient decent interpretation
Gradient descent는 함수를 2차 식으로 근사한 후 함수의 최소 위치를 다음 위치로 선택하는 방법이다.
이 과정을 보이기 위해 함수 \(f\)를 2차 Taylor 식으로 전개해보자.
\begin{align} f(y) \approx f(x) + \nabla f(x)^T (y - x) + \frac{1}{2} \nabla^2 f(x) \parallel y - x \parallel_2 ^2 \end{align}
이때 2차 항에 있는 hessian \(\nabla^2 f(x)\)를 \(\frac{1}{t}I\)로 대체하면 다음과 같이 표현된다. 여기서 \(t\)는 step size이다.
\begin{align} f(y) \approx f(x) + \nabla f(x)^T (y - x) + \frac{1}{2t} \parallel y - x \parallel_2 ^2 \end{align}
따라서, gradient descent에서는 step size의 역수가 eigenvalue인 hessian 행렬을 2차 항의 계수로 갖는 2차식으로 함수를 근사했다고 볼 수 있다. 또한, 이 식에서 \(f(x) + \nabla f(x)^T (y - x)\)는 \(f\)에 대한 선형 근사로 볼 수 있으며, \(\frac{1}{2t} \parallel y - x \parallel_2^2\)는 \(x\)에 대한 proximity term으로 볼 수 있다. Proximity term은 \(x\)에서 \(y\)가 얼마나 가까운지를 나타낸다.
이렇게 근사된 함수의 2차식을 최소화하는 위치를 다음 위치로 선택하게 된다. 그러기 위해 \(f(y)\)의 gradient를 0으로 두고 다음 위치인 \(y = x^+\)를 구하면 다음과 같은 식을 얻게 된다.
\[x^+ = x - t \nabla f(x)\]
아래 그림에서 파란색 점은 현재 위치 \(x\)를 나타내며 빨간색 점은s 다음 위치 \(y\)를 나타낸다. 아래쪽에 있는 곡선은 실제 함수 \(f\)의 곡선이며 윗쪽에 있는 곡선은 함수 \(f\)의 2차 근사 곡선이라고 볼 수 있다. 따라서, 빨간색 점은 2차 근사식에 대한 최소 지점을 나타낸다.
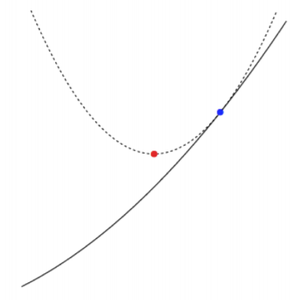
현재 위치 \(x\)에서 다음 위치 \(y\)가 얼마나 가까운지는 proximity term의 weight \(\frac{1}{2t}\)에 따라 달라진다. 만약 \(t\) 값이 작다면, proximity term의 weight는 커지게 되고 스텝은 작아지게 될 것이다. 이러한 과정은 다음 수식으로 표현된다.
\begin{align} x^+ = \underset{y}{\arg \min} \ f(x) + \nabla f(x)^T (y - x) + \frac{1}{2t} \parallel y - x \parallel_2^2 \end{align}