03-04-01 Definition and examples

Definition

함수 \(f: \mathbb{R}^n \rightarrow \mathbb{R}\)가 도메인 \(\text{dom}f\)와 모든 sublevel set \(S_{\alpha}\)(03-01-03 참고)이 convex라면 이 함수를 quasiconvex (or unimodal)이라고 한다.

\(f : \mathbb{R}^n \rightarrow \mathbb{R}\) is quasiconvex if \(\text{dom}f\) and \(S_{\alpha} =\{x \in \text{dom}f \mid f(x) \leq \alpha\}\) for \(\alpha \in \mathbb{R}\) are convex.

만약 함수 \(-f\)가 quasiconvex라면, \(f\)는 quasiconcave 라고 불린다.

\(f : \mathbb{R}^n \rightarrow \mathbb{R}\) is quasiconcave if \(\text{dom}f\) and \(S_{\alpha} = \{ x \in \text{dom}f \mid f(x) \geq \alpha \}\) for \(\alpha \in \mathbb{R}\)

\(f\)가 quasiconvex이고 quasiconcave일 때, 이를 quasilinear라고 하고, 함수의 도메인과 모든 level set에서 \(\{x \mid f(x)=\alpha\}\)는 convex가 된다. 다음 그림은 quasiconvex function의 예를 보여준다.

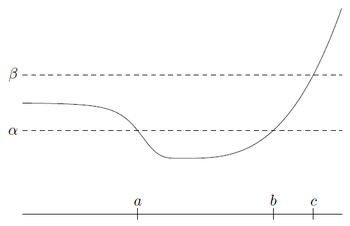
\(\alpha\)에 대하여, \(\alpha\)-sublevel set \(S_{\alpha}\)는 convex, 즉 interval \([a,b]\)이다. \(\beta\)-sublevel set \(S_{\beta}\)는 interval (\(-\infty,c\)]을 갖는다. Convex function은 convex sublevel set을 가지며, quasiconvex가 성립하지만, 그 역은 성립하지 않는다.

\(f\) : convex \(\Longrightarrow\) \(f\) : quasiconvex

Examples

Quasiconvex에서의 다양한 예제를 살펴보자.

Logarithm

\(R_{++}\)공간에서의 \(\log x\)는 quasiconvex이다. (또한 quasiconcave이므로, quasilinear의 성질을 갖는다.)

\(\log x\) on \(\mathbb{R}\)

Ceiling function

Ceiling function은 quasiconvex이다. (또한 quasiconcave 이다.)

\(\text{ceil}(x) = \inf \{z \in Z \mid z \geq x\}\)

Length of vector

\(x \in \mathbb{R}^n\)의 길이를 nonzero component의 가장 큰 index 값으로 놓는다면,

\(f(x) = \max\{i \mid x_i \neq 0\}\).

이 성립하며,

\(f(x) \leq \alpha \iff x_i = 0\) for \(i = \lfloor\alpha\rfloor + 1,...,n.\) on \(\mathbb{R}^n\)

의 subspace를 만족하므로, quasiconvex이다.
(※ subspace : subspace 내에 있는 모든 원소들은 덧셈, 곱셈에 대해 닫혀있다. \(\mathbb{R}^n\)의 subspace도 convex set 이다.)

Linear-fractional function

다음 조건에서, function \(f\) 는 quasiconvex이자 quasiconcave, 즉 quasilinear이다.

\(f(x) = \frac{a^Tx+b}{c^Tx+d}\) with \(\text{dom}f =\{x \mid c^Tx + d > 0\}\)

Distance ratio function

\(a, b \in \mathbb{R}^n\)이고, function \(f\)를 다음과 같이 정의할 때, 즉, x와 a 간의 유클리디안 거리와 x와 b 간의 유클리디안 거리의 비율을 나타내는 function \(f\)에서, \(f\)는 halfspace \(\{x \mid \parallel x - a \parallel_2 \leq \parallel x - b \parallel_2 \}\) 상에서 quasiconvex이다.

\(f(x) = \frac{ \parallel x - a \parallel_2 }{ \parallel x - b \parallel_2 }\)

\(\alpha \leq 1\) 조건에서, 이는 유클리디안 ball 형태의 convex set이 되므로 \(f\)는 quasiconvex가 된다.