03-01-03 Key properties of convex functions

Epigraph characterization

앞 1.2절에서 살펴본 바와 같이 \(f\)가 convex 이면 그 epigraph는 convex set이고, 그 역도 성립한다.

\(f\) is convex $$\iff epi(f) = {(x,t) \in \mathbb{R}^{n+1}

x \in \text{dom} f, f(x) \le t }$$ is a convex set

Convex sublevel sets

함수 \(f\)가 convex이면, 그 sublevel set 도 convex 이다.

\(\{x \in dom f: f(x) \leq t\}\), for all \(t \in \mathbb{R}\)

[참고] Sublevel set

함수의 \(f:\mathbb{R}^n \mapsto \mathbb{R}\)에 대한 \(C_\alpha = \{x \in \text{dom} f | f(x) \leq \alpha\}\)를 \(\alpha\)-sublevel set 이라고 한다.

First-order characterization

함수 \(f\)가 미분가능하다고 가정하면, 다음이 성립한다.
함수 \(f\)의 도메인 \(dom\) \(f\)가 convex이고, 함수 \(f\)의 도메인에 속하는 임의의 \(x, y\) 에 대하여 \(f(y) \geq f(x) +\nabla f(x)^T(y−x)\) 가 성립하면 함수 \(f\)는 convex 이며 그 역도 성립한다.

\(f\)is convex \(\iff \text{dom}f\) is convex, and \(f(y) \geq f(x) +\nabla f(x)^T(y−x)\) for all \(x,y \in \text{dom} f\)

아래 그림은 미분 가능한 convex function \(f\)에 관한 1차 테일러 다항식의 그래프이다. 임의의 \(x, y \in \text{dom} f\)에 대해서 \(f(y) \geq f(x) + \nabla f(x)^T(y-x)\) 임을 만족하는 것을 보여준다.

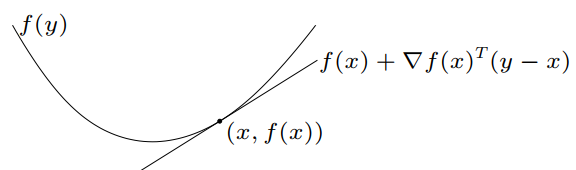
Second-order characterization

함수 \(f\)가 두번 미분가능할 때 함수 \(f\)는 다음과 같은 성질을 가진다.

• 정의역이 convex 인 함수 \(f\)의 2차 미분이 0보다 크거나 같을 경우, 함수 \(f\)는 convex 이며, 그 역 또한 성립한다.

\(f\) is convex \(\iff \nabla^2f(x) \succeq 0\) for all \(x \in \text{dom} f, \text{dom} f\): convex

• 함수 \(f\)의 2차 미분이 0보다 클 경우, 함수 \(f\)는 strictly convex 이다.

if \(\nabla^2f(x) \succ 0\) for all \(x \in \text{dom} f\), then \(f\) is strictly convex

• 즉 기울기의 변화가 항상 양수가 됨을 의미한다.

Jensen’s inequality

함수 \(f\)가 convex 이고 \(n\)개의 양수 \(w_1, ..., w_n\)에 대하여 \(\sum_{i=1}^{n} w_i = 1\) 이라 하자. 이 때 다음이 성립한다.

\(\sum_{i=1}^{n} w_i f(x_i) ≥ f \left ( \sum_{i=1}^{n} w_i x_i \right )\)

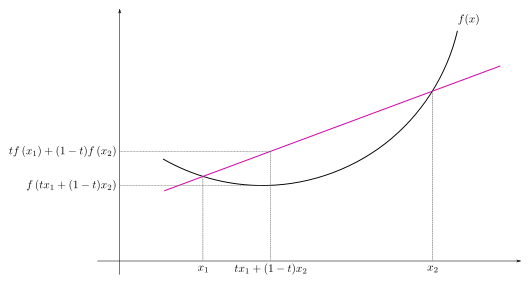
함수 \(f\)가 convex 이면 다음 부등식을 만족한다.

\[f(tx_1 + (1 − t)x_2) \le tf(x_1) + (1 − t)f(x_2) \text{ for } 0 \le t \le 1\]

Extension:
\(X\) is a random variable supported on \(\text{dom } f\), then \(f(E[X]) \le E[f(X)]\)