03-01-01 Definition

Convex function

함수 \(f:\mathbb{R}^n \rightarrow \mathbb{R}\)의 정의역이 convex set이고, 임의의 두점 \(x, y ∈dom\) \(f\)를 잇는 선분 위의 모든 점들이 함수 \(f\) 위의 점들보다 위에 있다면 그 함수 \(f\)는 convex 이다.

\(f(\theta x+(1− \theta)y) \le \theta f(x)+(1−\theta)f(y)\),

with \(\theta \le \theta \le 1\), for all \(x,y \in dom\) \(f\)

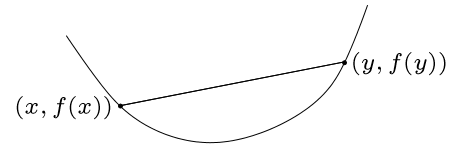
위의 식은 기하학적으로 [Fig1]에서 보는 것처럼 함수 \(f\)상에 존재하는 임의의 점 \(x\)와 점\(y\)를 잇는 선분이 함수 \(f\)의 그래프 위에 존재하는 것을 의미한다. 즉, 두 점 \(x,y\)의 convex combination에서의 \(f\)의 값은 \(f(x), f(y)\)의 convex combination의 값보다 작거나 같다.

Strictly convex

함수 \(f:\mathbb{R}^n \rightarrow \mathbb{R}\)가 임의의 서로 다른 두 점 \(x, y ∈dom\) \(f\) 과 \(0<θ<1\)에 대해 다음의 조건을 만족하면 이를 strictly convex 이라 한다.

\(f(\theta x+(1−\theta)y)<\theta f(x)+(1−\theta)f(y)\),

with \(0<\theta<1\), \(x \neq y\), for all \(x, y \in dom\) \(f\)

Strongly convex

\(f − {m \over 2}\left \lVert x \right \rVert_{2}^{2}\), with \(m > \theta\) 가 convex 이면 \(f\)는 strongly convex이다.

[Note] strongly convex ⇒ strictly convex ⇒ convex

Concave function

함수 \(-f\)가 convex이면, \(f\)는 concave라고 한다.

Linear 함수를 포함한 모든 affine 함수 \(f(x) = a^T x+b\) 는 다음 식을 만족한다.

\(\begin{aligned} f(\theta x+(1−\theta)y) &= a^T (\theta x+(1−\theta)y) +b \\ &= \theta a^T x + (1−\theta) a^T y + \theta b + (1−\theta) b \\ &= \theta f(x)+(1−\theta)f(y) \\\\ \end{aligned}\) \(\text{for all } x,y \in \text{dom } f, \text{with} \theta \le \theta \le 1\)

즉, affine 함수는 항상 convex이며, 동시에 concave 이다.