02-01-01 Line, line segment, ray

Affine set, convex set, cone을 정의하기 위해 먼저 직선(line), 선분(line segment), 반직선(ray)을 먼저 살펴보자.

Line은 두 점을 지나면서 양쪽 방향으로 무한히 커지는 선을 말한다. 반면, line segment는 두 점 사이에서만 정의되는 선을 말하며, ray는 한 점에서 시작해서 다른 점을 지나면서 무한히 커지는 선을 말한다. 다음 그림에서는 line과 line segment를 보여주고 있다. 파라미터 $\theta$의 범위에 따라 line, line segment, ray가 어떻게 정의될 지 상상해보라.

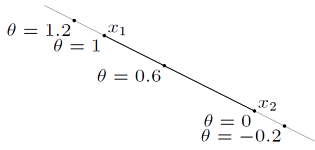
[참고] Set에 포함된 임의의 두 점을 이용해서 line 또는 line segment, ray를 만들었을 때, 이들이 set에 포함되는지 여부로 set을 정의하게 된다. (이때 set을 여러 점으로도 정의할 수 있는데, set에 포함된 여러 점들을 이용해서 affine combination, convex combination, conic combination 했을 때 그 결과가 set에 포함되는지 여부로 정의하게 된다. 자세한 내용은 뒷 절에서 설명할 것이다.)

Line

두 점 $x_1$과 $x_2$을 지나는 Line은 다음과 같이 정의된다. 이때, $\theta$는 임의의 실수이며 $\theta$가 0이면 $y$는 $x_2$가 되고, $\theta$가 1이면 $y$는 $x_1$이 된다. 따라서, $\theta$가 0보다 작거나 1보다 크면 $x_2$에서 $x_1$까지의 범위를 벗어나는 것을 위의 그림에서 확인할 수 있다.

$y=\theta x_1+(1-\theta )x_2$ with $\theta \in \mathbb{R}$

Line segment

직선의 식에서 $\theta$의 범위를 0에서 1로 제한하면 line segment가 된다. 따라서, line segment는 직선의 식에 $0\le \theta \le 1$ 조건을 추가해서 정의할 수 있다.

$y=\theta x_1+(1-\theta )x_2$ with $0\le \theta \le 1$

다음과 같이 식을 조금 다르게 표현해서 해석해보면 line segment는 점 $x_2$에서 출발해서 $(x_1-x_2)$ 벡터 방향으로 $\theta$배로 진행하다 $x_1$에 도달하면 멈추는 것으로 생각해볼 수 있다.

$y=x_2+\theta (x_1-x_2)$ with $0\le \theta \le 1$

Ray

Ray는 한 점에서 시작해서 다른 점을 지나면서 무한히 커지는 직선을 말한다. 점 $x_2$에서 출발해서 $(x_1-x_2)$ 벡터 방향으로 $\theta$배로 무한히 진행한다.

$y=x_2+\theta (x_1-x_2)$ with $\theta \ge 0$

이 식을 다음과 같이 정리해 보면 위의 line과 line segment 식과 $\theta$의 조건만 다르고 동일한 형태임을 알 수 있다.

$y=\theta x_1+(1-\theta )x_2$ with $\theta \ge 0$

이제 $\theta$의 범위가 line은 $\theta \in \mathbb{R}$, line segment는 $0\le \theta \le 1$, ray는 $\theta \ge 0$라는 것을 알 수 있다. 또한, 앞으로 정의하게 될 affine set, convex set, conic set에서도 $\theta$의 범위도 동일하다는 것을 알게 될 것이다.