01-03 Goals and Topics

Goals

앞으로의 학습과정을 통해 다음과 같은 능력이 배양되는 것을 목표로 한다.

• 주어진 문제상황이 convex optimization problem에 해당함을 파악(recognize)
• 주어진 문제상황을 convex optimization problem으로 표현(formulate)
• 정의된 convex optimization problem을 풀기위한 가장 적절한 알고리즘을 선택

Topics

위와 같은 목표를 달성하기 위해 다음과 같은 주제들이 다룰 것이다.

• convex sets, functions, optimization problems
• examples and applications
• algorithms

특히 위의 주제들 중에서, algorithm에 대한 내용이 주를 이루게 될 것이다.

Algorithms

보통 최적화 문제를 풀기 위해서는 굉장히 다양한 방법이 적용될 수 있다. 서로 다른 방법들은 각각 정의된 문제의 성질에 따라 성능이 달라질 수 있다. 즉, 문제를 해결하기 가장 효율적인 알고리즘을 선택하기 위해서는 주어진 문제와 각 알고리즘에 대한 깊은 이해가 필요하다. Total variation denoising을 예로 들어보자.

Example: Total variation denoising

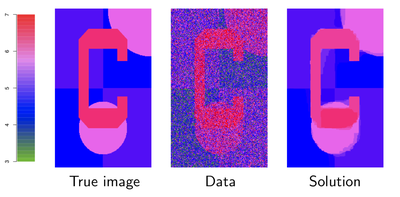
노이즈가 잔뜩 낀 이미지 Data(중간)를 받았을 때, 그 이미지에서 노이즈를 제거하고 True Image(좌측)에 가까운 Solution(우측)을 얻고 싶은 상황이라고 가정하자. 각 pixel값을 \(y_i, i = 1, ..., n\)라고 한다면 이 문제는 다음과 같은 최적화 문제로 정의될 수 있으며, 이는 보통 2d fused lasso 또는 2d total variation denoising problem으로 불린다.

\[\min_{\theta} \frac{1}{2} \sum_{i=1}^n (y_i - \theta_{i})^2 + \lambda \sum_{(i,j) \in E} \vert \theta_i - \theta_j \vert\]

• E: 인접한 모든 \(\theta\) 사이의 Edge들을 모아둔 집합
• \(\frac{1}{2} \sum_{i=1}^n (y_i - \theta_{i})^2\): Least squares loss. \(\theta\)가 \(y\)에 가까워지게 한다.
• \(\sum_{(i,j) \in E} \vert \theta_i - \theta_j \vert\): Total variation smoothing. 인접한 pixel 간 값의 변화가 이미지 전반에 거쳐 그리 많지 않을때 (piecewise constant) 이용할 수 있는 방법이다. 이와 같이 올바른 smoothing 기법의 선택을 위해서는 대상의 특성이 충분히 고려되어야 한다. (Total variation smoothing에 대한 더 자세한 설명은 참고문헌 1의 챕터 6.1.2와 6.3에서 볼 수 있다.)

앞서 정의된 convex optimization problem은 Specialized ADMM 알고리즘을 이용하면 20번의 iteration으로 우측과 같은 solution을 얻을 수 있다.

Specialized ADMM, 20 iterations

Proximal gradient descent, 1000 iterations

Coordinate descent, 10K cycles

위 결과에서 알 수 있듯이 2d fused lasso problem에 대해서는 세 가지 방법 중 Specialized ADMM이 가장 좋은 성능을 발휘한다. 하지만 문제가 달라지면 다른 두 방법이 Specialized ADMM을 압도하는 경우도 발생할 수 있다. 이후의 챕터에서는 다양한 알고리즘과 문제를 분석하여 적절한 알고리즘을 선택하는 방법에 대해 알아볼 것이다.