01-02 Convex optimization problem

Convex optimization problem은 optimization problem의 한 종류이다.

\[\begin{align*} &\min_{x\in D}\ &&f(x) \\ &\text{subject to} && g_i(x) \le 0,\ i = 1, ..., m \\ &&& h_j(x) = 0,\ j = 1,\ ..., r \end{align*}\]

Convex Optimization Problem in standard form [3]

여기서 objective function \(f\)와 inequality constraint function \(g_i\)가 convex이고, equality constraint function \(h_j\)가 affine이라는 조건이 추가된다. 이때 affine function이란 다음과 같이 linear function에 상수합이 붙은 형태의 함수를 의미한다.

\(h_j,\ j = 1, ..., r\) are affine: \(h_j(x) = a_{j}^T x + b_{j},\ j=1, ..., r\)

그렇다면 convex function은 어떤 함수를 의미하는 것일까? 이를 이해하기 위해서 convex set을 이해할 필요가 있다.

Convex sets

두 점 \(x_1\)과 \(x_2\)를 잇는 선분(line segment)은 다음과 같이 정의된다.

\(x = \theta x_1 + (1 - \theta) x_2\) with \(0 \le \theta \le 1\)

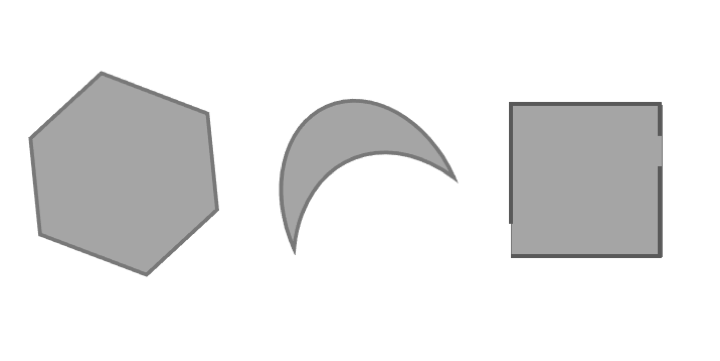
어떤 집합(set)이 주어져 있다고 하자. 이 집합의 원소인 두 점 \(x_1\)과 \(x_2\)를 잇는 선분이 이 집합에 다시 포함될때 우리는 이 집합을 convex set이라고 부른다. 다시 말하면 집합 C가 convex가 될 조건은 다음과 같다.

\(x_1, x_2 \in C\), \(0 \le \theta \le 1\) \(\Rightarrow\) \(\theta x_1 + (1-\theta)x_2 \in C\)

예를 들어, 다음 세 가지 그림 중 가장 좌측의 그림만이 convex set에 해당한다.

Convex functions

Convex function은 다음과 같이 정의된다.

\(f: R^n \rightarrow R\) is convex if \(dom(f)\) is a convex set and,

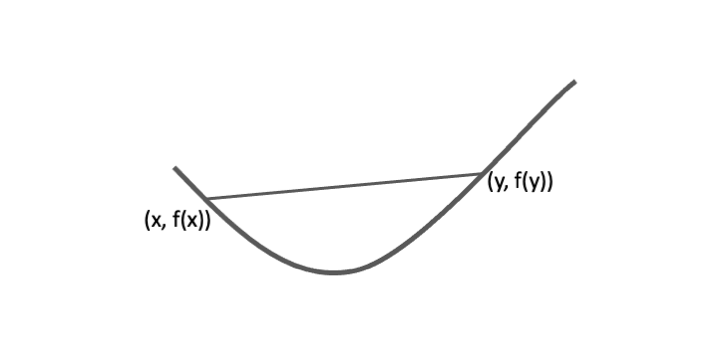
\(f(\theta x + (1 - \theta)y) \le \theta f(x) + (1-\theta)f(y)\) for all \(x, y \in dom(f),\ 0 \le \theta \le 1\)

정의에서 부등식으로 표현된 조건은 다음과 같은 기하학적 의미를 가진다. \(f\)의 그래프 상의 임의의 두 점 \((x,\ f(x))\), \((y,\ f(y))\)을 생각해보자. 이 두 점을 잇는 선분은 구간 \([x, y]\)에서 그래프보다 크거나 같게 위치한다.

Relation between a convex set and a convex function

convex function과 convex set 사이에는 다음과 같은 밀접한 관계가 있다.

함수 \(f\)의 epigraph가 convex set일때, 함수 \(f\)는 convex function이다.

여기서 epigraph는 무엇을 의미하는 것일까? Epigraph에서 ‘Epi’는 ‘above’를 뜻하며, 곧 epigraph는 ‘above the graph’를 의미한다. 즉, epi \(f\)란 \(f\)의 그래프의 위쪽 영역에 해당하는 집합이다. 함수 epigraph는 다음과 같이 정의한다.

\[\eqalign{ & \text{epigraph of } f: R^n \rightarrow R\\ & \text{epi } f = \{(x, t) \in R^{n+1} \mid x \in \text{ dom } f, f(x) \le t\} }\]

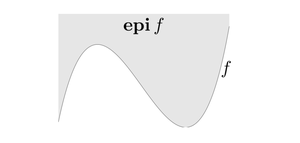
함수 f가 convex function일때 epi f는 항상 convex set이고 이의 역도 성립한다. 이를 주지하고 위의 convex function과 convex set의 정의를 다시 한번 살펴보도록 하자.

Nice property of convex optimization problems

Convex 함수의 local minimum은 항상 global minimum이다. convex optimization problem의 경우 non-convex optimization problem에 비해 일반적으로 solution을 더 쉽게 구할 수 있는데, 그 이유는 convex 함수가 다음과 같은 특성을 가지기 때문이다.

\(f\)가 convex이고 \(x\)가 \(f(x)\)의 locally optimal point일 때(즉 \(f(x)\)가 local minimum), x는 globally optimal point이다.

이를 한번 증명해보자.

proof by contradiction:

Convex function f에 대해 \(x\)가 globally optimal이 아닌 locally optimal point라고 하자. 또, feasible \(y\)를 global optimal point라고 하면, \(y\)는 임의의 양수 \(\rho\)에 대해 \(\|y - x\|_2 > \rho\)이고, \(f(y) < f(x)\)이 성립한다. (왜냐하면, \(x\)가 locally optimal이므로 \(\|x - y\|_2 \le \rho\) 이면 \(f(x) \le f(y)\)이기 때문이고, 이는 \(y\)가 global optimal point임에 위배된다.) 이때, \(\theta=\frac{\rho}{2\|y-x\|_2}\)에 대해 \(z = \theta y + (1 - \theta) x=x + \theta( y - x)\)라고 하면, 다음이 성립한다.

1.\(\phantom{1} z\)는 두 개의 feasible points \(x, y\)에 대한 convex combination이므로 또한 feasible하다.

2.\(\phantom{1}\|z - x\|_2 = \theta \|y - x\|_2 = \frac{\rho}{2} < \rho\) 이다.

3.\(\phantom{1} f(z) \le \theta f(y) + (1 - \theta) f(x) < \theta f(x) + (1 - \theta) f(x) = f(x)\)

2,3는 \(x\)가 locally optimal point이기 위한 전제조건 \(f(x) < f(z)\)에 대한 모순이므로 귀류법에 의해 locally optimal point \(x\)가 곧 globally optimal point이다.

convex combination

\(x_1, ..., x_k\)에 대한 convex combination x는 다음과 같이 정의된다.

\(x = \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_k x_k\) with \(\theta_1 + \cdots + \theta_k = 1, \theta_i \ge 0\)

\(D\)가 convex set일때 \(x_1, x_2, ..., x_k \in D\)이면, \(x \in D\)이다.